karush
Gold Member
MHB
- 3,240
- 5
(a) find solution of initial value and (c) interval
$$\quad\displaystyle
y^2(1-x^2)^{1/2} \,dy = \arcsin{x}\,dx,
\quad y(0) = 1$$
separate
$$y^2 \,dy = \frac{\arcsin{x}}{(1-x^2)^{1/2}}\,dx,$$
Integrate
\begin{align*}
\int y^2 \,dy& = \int\frac{\arcsin{x}}{\sqrt{(1-x^2)}}\,dx,
\end{align*}
ok I assume a trig substitution to solvebook answer
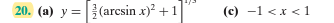
$$\quad\displaystyle
y^2(1-x^2)^{1/2} \,dy = \arcsin{x}\,dx,
\quad y(0) = 1$$
separate
$$y^2 \,dy = \frac{\arcsin{x}}{(1-x^2)^{1/2}}\,dx,$$
Integrate
\begin{align*}
\int y^2 \,dy& = \int\frac{\arcsin{x}}{\sqrt{(1-x^2)}}\,dx,
\end{align*}
ok I assume a trig substitution to solvebook answer
Last edited: