Jimmy87
- 692
- 19
- Homework Statement
- Determining velocity after a 2-D impact.
- Relevant Equations
- p = mv
Hi,
Here is the problem
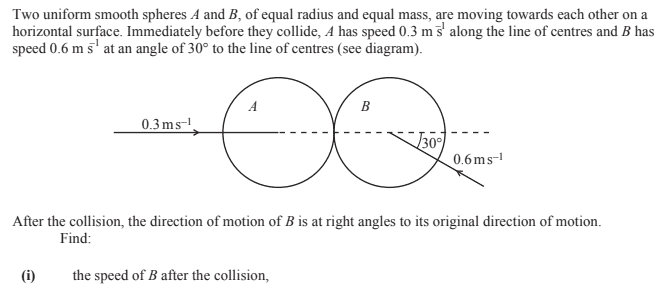
What is required to answer this question is two assumptions. Firstly, the component of the momentum normal to the centre line is the same before and after. Therefore, secondly, A must recoil entirely in the horizontal plane. This is the only way to answer this question and I can get the answer (0.34 m/s which I know to be correct). How do we know after this collision A is confined to the horizontal plane? Thanks.
Here is the problem
What is required to answer this question is two assumptions. Firstly, the component of the momentum normal to the centre line is the same before and after. Therefore, secondly, A must recoil entirely in the horizontal plane. This is the only way to answer this question and I can get the answer (0.34 m/s which I know to be correct). How do we know after this collision A is confined to the horizontal plane? Thanks.