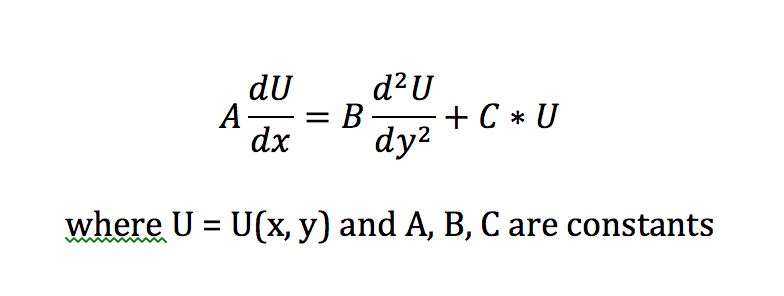Discussion Overview
The discussion revolves around solving a second-order partial differential equation (PDE) using the similarity method. Participants explore various approaches to derive solutions, particularly focusing on the diffusion reaction equation and its characteristics.
Discussion Character
- Exploratory
- Technical explanation
- Mathematical reasoning
Main Points Raised
- One participant describes an attempt to use a similarity solution method with the substitution eta = y/f(x) but reports difficulties when including a term involving C * U.
- Another participant clarifies the form of the PDE, suggesting it can be expressed in a standard format involving partial derivatives.
- A later reply proposes that if A is not equal to zero, the equation can be rewritten to highlight its nature as a diffusion reaction equation.
- One participant inquires about the existence of closed-form solutions for the diffusion reaction equation with a specific reaction term R(U) = C * U/A.
- Another participant suggests a substitution that transforms the original equation into a standard diffusion equation.
Areas of Agreement / Disagreement
Participants present various methods and transformations related to the PDE, but there is no consensus on a single approach or solution. Multiple competing views and techniques are discussed without resolution.
Contextual Notes
Some assumptions about the parameters and the form of the PDE are not fully articulated, and the discussion includes unresolved mathematical steps related to the proposed transformations.
Who May Find This Useful
Readers interested in advanced mathematical methods for solving PDEs, particularly in the context of diffusion and reaction equations, may find this discussion relevant.