4 part problem about a 4-sided die.

  • Context: MHB 
  • Thread starter Thread starter Angelaa
  • Start date Start date
Click For Summary

Discussion Overview

The discussion revolves around a problem involving a 4-sided die rolled twice, focusing on calculating the products of the results from the two rolls. Participants explore how to construct a grid to represent these products, identify the sample space of possible products, and determine the number of distinct outcomes. The scope includes mathematical reasoning and conceptual clarification related to probability and combinatorics.

Discussion Character

  • Exploratory
  • Mathematical reasoning
  • Conceptual clarification
  • Homework-related

Main Points Raised

  • Some participants express confusion about the problem's requirements, particularly regarding the grid and the products of the two dice.
  • One participant suggests that the grid should represent the product of the results from the first and second die, with specific examples provided for clarity.
  • Visual aids are offered to help others understand how to fill in the grid based on the multiplication of die results.
  • There is a discussion about the sample space, with participants attempting to identify the unique products that can result from the two rolls.
  • Some participants propose different sets for the sample space, with ongoing corrections and refinements to the proposed answers.
  • Clarifications are made regarding the need to list unique products without repetition, leading to further exploration of what constitutes the sample space.
  • Participants express uncertainty about the cardinality of the sample space and the most frequent outcomes, with multiple suggestions and corrections made throughout the discussion.

Areas of Agreement / Disagreement

Participants do not reach a consensus on the exact answers to the questions posed in the problem, as there are multiple interpretations and corrections regarding the sample space and the outcomes. The discussion remains unresolved with various competing views on the correct approach.

Contextual Notes

Participants highlight the importance of distinguishing between unique products and total outcomes, leading to some confusion about how to accurately represent the sample space. There are also references to potential ambiguity in the wording of the problem, which may affect participants' understanding.

Who May Find This Useful

This discussion may be useful for students learning about probability, combinatorics, and mathematical reasoning, particularly those encountering similar problems involving dice and sample spaces.

Angelaa
Messages
9
Reaction score
0
Alright, so I guess I'm confused as to what the problem is asking me to do.

This is the problem. I'll write exactly as it's shown.

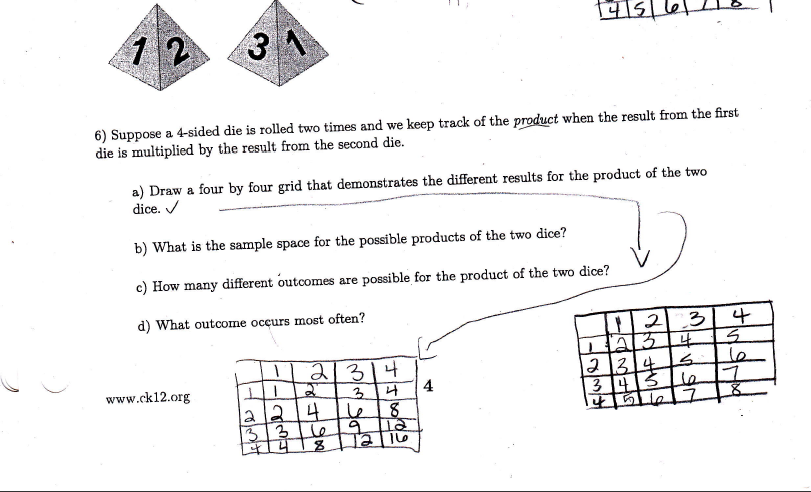
Suppose a 4-sided die is rolled two times and we keep track of the product when the result from the first two die is multiplied by the result from the second die.

A) Draw a four by four grid that demonstrates the different results for the product of the two dice.

B) What is the sample space for the possible products of the two dice?

C) How many different outcomes are possible for the product of the two dice?

D) What outcome occurs most often?I started out fine. I drew the first four by four grid, but after that I was completely lost. What do they mean when they're asking for the different results for the product of the two dice? What numbers am I supposed to put in the second grid? The rest of the questions are hard for me to answer, too.

Please help.
 
Physics news on Phys.org
I'm guessing the problem should actually state:

Suppose a 4-sided die is rolled two times and we keep track of the product when the result from the first die is multiplied by the result from the second die.

A) Let the column number represent the result for the first die, and the row number represent the result from the second die, and then each entry in the grid or array will then be the product of the row and column numbers. For example, the upper left entry would be the product $1\,\times\,1=1$ while the lower right would be $4\,\times\,4=16$. Can you fill in the rest?
 
Hi Angelaa, :)

Welcome to MHB!

Not trying to highjack the thread, but just want to provide a visual based on MarkFL's explanation. If you are a more visual person this might help you see how you can use his suggestion to help you understand the problem.

[table="width: 500, class: grid"]
[tr]
[td][/td]
[td]Die 1 rolls 1[/td]
[td]Die 1 rolls 2[/td]
[td]Die 1 rolls 3[/td]
[td]Die 1 rolls 4[/td]
[/tr]
[tr]
[td]Die 2 rolls 1[/td]
[td][math]1 \times 1 = 1[/math][/td]
[td][/td]
[td][/td]
[td][/td]
[/tr]
[tr]
[td]Die 2 rolls 2[/td]
[td][/td]
[td][/td]
[td][/td]
[td][/td]
[/tr]
[tr]
[td]Die 2 rolls 3[/td]
[td][/td]
[td][/td]
[td][/td]
[td][/td]
[/tr]
[tr]
[td]Die 2 rolls 4[/td]
[td][/td]
[td][/td]
[td][/td]
[td][math]4 \times 4 = 16[/math][/td]
[/tr]
[/table]
 
MarkFL said:
I'm guessing the problem should actually state:

Suppose a 4-sided die is rolled two times and we keep track of the product when the result from the first die is multiplied by the result from the second die.

A) Let the column number represent the result for the first die, and the row number represent the result from the second die, and then each entry in the grid or array will then be the product of the row and column numbers. For example, the upper left entry would be the product $1\,\times\,1=1$ while the lower right would be $4\,\times\,4=16$. Can you fill in the rest?

So the first part of the problem would look like this?

Screenshot2013-03-18at95218PM_zpse3a8cbae.png
 
Jameson said:
Hi Angelaa, :)

Welcome to MHB!

Not trying to highjack the thread, but just want to provide a visual based on MarkFL's explanation. If you are a more visual person this might help you see how you can use his suggestion to help you understand the problem.

[TABLE="class: grid, width: 500"]
[TR]
[TD][/TD]
[TD]Die 1 rolls 1[/TD]
[TD]Die 1 rolls 2[/TD]
[TD]Die 1 rolls 3[/TD]
[TD]Die 1 rolls 4[/TD]
[/TR]
[TR]
[TD]Die 2 rolls 1[/TD]
[TD][math]1 \times 1 = 1[/math][/TD]
[TD][/TD]
[TD][/TD]
[TD][/TD]
[/TR]
[TR]
[TD]Die 2 rolls 2[/TD]
[TD][/TD]
[TD][/TD]
[TD][/TD]
[TD][/TD]
[/TR]
[TR]
[TD]Die 2 rolls 3[/TD]
[TD][/TD]
[TD][/TD]
[TD][/TD]
[TD][/TD]
[/TR]
[TR]
[TD]Die 2 rolls 4[/TD]
[TD][/TD]
[TD][/TD]
[TD][/TD]
[TD][math]4 \times 4 = 16[/math][/TD]
[/TR]
[/TABLE]
I started to say "think of the multiplication table you learned in elementary school" but that's a much better way to demonstrate it. (Yes)
 
Angelaa said:
So the first part of the problem would look like this?

Screenshot2013-03-18at95218PM_zpse3a8cbae.png

Your grid on the left is what I believe is you are to compose. What does the other grid represent?

edit: Never mind, I see this is the sum, not the product of the two dice.
 
MarkFL said:
I started to say "think of the multiplication table you learned in elementary school" but that's a much better way to demonstrate it. (Yes)

Thank you (Nod) I really appreciate it!

Another couple questions though: so for the sample space question, would I answer it like this?

s = {2, 3, 4, 5, 6, 7, 8} and s = {1, 2, 3, 4, 5, 6, 7, 8, 9 , 10, 11, 12, 13, 14, 15, 16}

and for the outcome question, would the answer be 16?

I'm really sorry. I just began my class today and I'm a little slow when it comes to math so I'm sure this must seem really easy and extremely basic to you!
 
The sample space is the set of all possible outcomes.

Now, you are only being asked about the product so just use the grid you drew on the left. What elements are present, traditionally listed in ascending order, without repeating any elements?

Yes, the total number of outcomes is $4\,\times\,4=16$, but some of them are repeated. You are being asked for the number of distinct elements in the sample space.

And there is no need to apologize for just having began your statistics course. Every single one of us had our first day too. You are doing well...you are showing your work and making a genuine effort to understand the problem. :D
 
Last edited:
MarkFL said:
The sample space is the set of all possible outcomes.

Now, you are only being asked about the product so just use the grid you drew on the left. What elements are present, traditionally listed in ascending order, without repeating any elements?

Yes, the total number of outcomes is $4\,\times\,4=16$, but some of them are repeated. You are being asked for the number of distinct elements in the sample space.

And there is no need to apologize for just having began your statistics course. Every single one of us had our first day too. You are doing well...you are showing your work and making a genuine effort to understand the problem. :D
Hmm...so... s = {8 x 2} ? I know that might not be right. Am I at least on the right track?

And thank you! I really appreciate your words and help.
 
  • #10
The sample space for the possible products would be the set of unique products that are possible. Referring to your grid, can you list these products in ascending order as a set?
 
  • #11
MarkFL said:
The sample space for the possible products would be the set of unique products that are possible. Referring to your grid, can you list these products in ascending order as a set?

Oh! I think I see what you're saying. So s = {1,4,9,16}??
 
  • #12
Angelaa said:
Oh! I think I see what you're saying. So s = {1,4,9,16}??

Those are some of the possible products but there are some more. You filled out the table correctly first of all. :) So now you should add the missing terms into your sample space. 1,4,9 and 16 are all in there but what about 3, 6 or 12? Any others? Basically you should list all of the values you filled into the table you drew, but just don't list anything more than once.

What do you get when you try that?
 
  • #13
Jameson said:
Those are some of the possible products but there are some more. You filled out the table correctly first of all. :) So now you should add the missing terms into your sample space. 1,4,9 and 16 are all in there but what about 3, 6 or 12? Any others? Basically you should list all of the values you filled into the table you drew, but just don't list anything more than once.

What do you get when you try that?
Ohh, see I thought he meant that you just list out the unique numbers- the ones that aren't seen more than once in the table.

So it would be like: s = {1,2,3,4,6,8, 9, 12, 16}, right??

I hope that's right, lol. Thank you for being patient with me as I try to figure this out!
 
  • #14
Yes, that's correct. (Yes) I do apologize for the ambiguity in my choice of words. I did mean to list each outcome with no repeating of the elements that occur more than once.

So, how many elements are in the sample space (called the cardinality of the set)? This is what part c) is asking.
 
  • #15
MarkFL said:
Yes, that's correct. (Yes) I do apologize for the ambiguity in my choice of words. I did mean to list each outcome with no repeating of the elements that occur more than once.

So, how many elements are in the sample space (called the cardinality of the set)? This is what part c) is asking.

No, do not be sorry! You've been a superb help and I really appreciate it! When it comes to math, I don't always understand things right away so that's probably why I didn't quite see what you were saying.

That answer would be 16, right? :) And for the outcome question, would it be 5 or is the first table on the right completely irrelevant? If it is irrelevant, I'm assuming the most frequently occurring outcomes are 2, 3, 4, 6, 8, and 12- although the question didn't ask for outcomes, just outcome...so that assumption could be entirely wrong, lol.
 
  • #16
I can completely understand how what I said could be interpreted the way you did. It was a poor choice of words on my part.

In the sample space you correctly gave:

S = (1, 2, 3, 4, 6, 8, 9, 12, 16}

How many elements are in this set?

How many times does each element show up in your grid?

And yes, the second grid is irrelevant, unless you are being asked also about the sums of the two dice.
 
  • #17
MarkFL said:
I can completely understand how what I said could be interpreted the way you did. It was a poor choice of words on my part.

In the sample space you correctly gave:

S = (1, 2, 3, 4, 6, 8, 9, 12, 16}

How many elements are in this set?

How many times does each element show up in your grid?

And yes, the second grid is irrelevant, unless you are being asked also about the sums of the two dice.

Ah, so 9!

And for most of them, twice. 2, 3, 4, 6, 8, and 12 show up twice in the grid. The other numbers only show up once. Are those the numbers the answer?
 
  • #18
Yes, 9 is the cardinality of the sample space! :cool:

Look at your grid again...you'll see one of the outcomes occurs 3 times. Can you find which one?
 
  • #19
MarkFL said:
Yes, 9 is the cardinality of the sample space! :cool:

Look at your grid again...you'll see one of the outcomes occurs 3 times. Can you find which one?

Oh my goodness, I feel so stupid! 4! (Giggle)

I'm so sorry I missed that! Thank you for all of your help and for being patient with me! You have no idea how much I appreciate your help.
 
  • #20
Yes, you are correct! (Rock)

We are happy to help here, particularly when the person posting makes a good effort such as you have shown. Congratulations for sticking through to the end and correctly answering all 4 parts of the problem! (Clapping)
 

Similar threads

Undergrad Probability to get a certain number or less by throwing two 6-faced die
  • · Replies 6 ·
Replies
6
Views
2K
MHB Pr of exactly one dice showing 2
  • · Replies 9 ·
Replies
9
Views
3K
MHB Find the probability all 5 dice rolls are the same
  • · Replies 2 ·
Replies
2
Views
4K
MHB Average "Hits" on exploding dice
  • · Replies 3 ·
Replies
3
Views
2K
MHB Probability: twice the same number
  • · Replies 10 ·
Replies
10
Views
2K
MHB S.aux.26 our-sided die has three blue faces, and one red face.......
  • · Replies 2 ·
Replies
2
Views
4K
High School A whole bunch of dice -- Statistics riddle
  • · Replies 2 ·
Replies
2
Views
2K
High School Probability in a dice game
  • · Replies 41 ·
2
Replies
41
Views
6K
Dice Game: 6-sided die vs 20-sided die
  • · Replies 53 ·
2
Replies
53
Views
10K
Graduate Can I Predict the Correct Dice Using Probability Distributions?
  • · Replies 3 ·
Replies
3
Views
1K