A question about multiresolution analysis (from a topological point of view)

[Lajka]

Hi,

I have a problem understanding something

This is a snapshot of a book I am reading

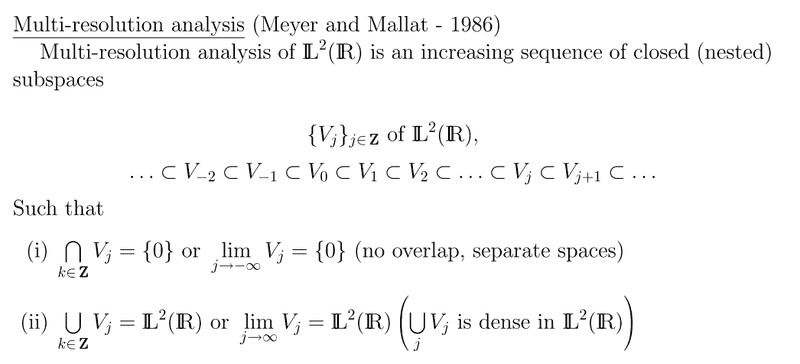
Point no. 2 concerns me, because it looks to me like it contradicts itself, with "this or this"

The first part says

\sum_{j}V_j = \mathbb{L^2(R)} which, to me, looks completely equivavalent to
\lim_{j \rightarrow \infty}V_j = \mathbb{L^2(R)}
given the nested nature of these subspaces.

However, the paper says

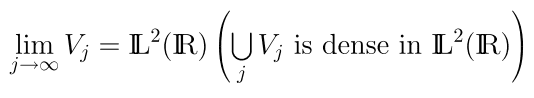
so what troubles me is this: is this countable union \sum_{j}V_j equal to \mathbb{L^2(R)} or is it only dense in \mathbb{L^2(R)}?

I personally think it's the former, and I don't understand this "dense" part. Could someone perhaps clarify this for me?

Much obliged!

 

[lavinia]

http://en.wikipedia.org/wiki/Multiresolution_analysis

I think the article says dense is correct

 

[Lajka]

Yes, it does. I had trouble understanding it, but I think I make some progress. I actually think now I may got it wrong from the very beginning.

E.g., if you have a family of functions {f_n} that has a limit f, I think it's okay to say that "lim(n→∞)=f" as well as "family {f_n} can approach arbitrarily close to f", because it's basically the same statement.

In the same manner, I now think it's equivalent to say "lim(n→∞) V_n = L2 (R)" or "union V_n can approach arbitrarily close to L2 (R)".