evinda
Gold Member
MHB
- 3,741
- 0
Hello! (Wave)
I want to apply the Dijkstra algorithm at an example.
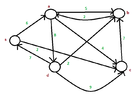
This is the given graph:
View attachment 3127
Executing the algorithm,I found the following:
$$p[a]=s$$
$$p[c]=s$$
$$p=c$$
$$p[d]=a$$
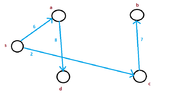
So,the tree,that we get from the Dijkstra's algorithm would be:
View attachment 3128
So,the weight would be $23$.
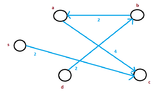
But...I found the following tree,with less weight:
View attachment 3129
Have I done something wrong,applying the algorithm? (Thinking)
I want to apply the Dijkstra algorithm at an example.
Code:
Dijkstra(G,s,v)
1. InitialValues(G,s)
2.S<-∅
3.Q<-V // priority queue,with key the field d[]
4. while Q ≠ ∅
5. u<-Extraction_of_Minimum(Q)
6. S<-S U {u}
7. for each v ∈ Adj[u]
8. Relaxation(u,v,w)
Code:
InitialValues(G,s)
for each v ∈ V
d[v]<-oo
p[v]<-∅
d[s]<-0
Code:
Relaxation(u,v,w)
if d[v]>d[u]+w(u,v)
d[v]<-d[u]+w(u,v)
p[v]<-uThis is the given graph:
View attachment 3127
Executing the algorithm,I found the following:
$$p[a]=s$$
$$p[c]=s$$
$$p=c$$
$$p[d]=a$$
So,the tree,that we get from the Dijkstra's algorithm would be:
View attachment 3128
So,the weight would be $23$.
But...I found the following tree,with less weight:
View attachment 3129
Have I done something wrong,applying the algorithm? (Thinking)
Attachments
Last edited: