Areas of a series of annular sectors

In summary, the conversation discussed a problem with finding the ratio of areas in a disc and whether it can be proven that A4/A3 > A3/A2 > A2/A1. The conversation also shared a humorous equation found on a bathroom wall. However, in the end, an idealized example showed that A4/A3 < A3/A2.
  • #1
jfox
2
0
Hi all

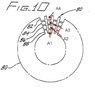
Hoping someone can figure out a problem. In the attached figure, A is the area of openings in a disc. Assume the segments 82, 84, 86, 88 are along a radius and are equal. Is it possible to prove that A4/A3 > A3/A2 > A2/A1?


In thanks I'll share this, hope it's not old news. Some wit wrote it on a bathroom wall when I was an undergrad, I still think it's funny.


[itex]\sqrt{(Doing)^{2} + (Being)^{2}}[/itex]= [itex]Doobee\,Doobee\,BingDing[/itex]

J Fox
 

Attachments

  • Series of Sectors.jpg
    Series of Sectors.jpg
    20.6 KB · Views: 420
Mathematics news on Phys.org
  • #2
Never mind. Trying an idealized example of r=R, .75R, .5R, .25R it comes down to

A4[itex]\propto[/itex] 12-.752
A3[itex]\propto[/itex] .752-.52
A2[itex]\propto[/itex] .52-.252

A4/A3 < A3/A2

But it was cool to find the math font/language!
 
Last edited:

1. What is an annular sector?

An annular sector is a portion of an annulus, which is a region between two concentric circles. It is defined by two radii, an inner radius and an outer radius, as well as an angle.

2. How do you find the area of an annular sector?

To find the area of an annular sector, you can use the formula A = (π/180) * r2 * θ, where r is the radius of the inner circle and θ is the central angle in degrees.

3. Can you find the area of an annular sector if the central angle is in radians?

Yes, you can use the formula A = (1/2) * r2 * θ, where r is the radius of the inner circle and θ is the central angle in radians.

4. How is an annular sector different from a regular sector?

An annular sector has two radii, an inner and an outer, while a regular sector only has one radius. Additionally, an annular sector is a portion of an annulus, while a regular sector is a portion of a circle.

5. What are some real-life applications of annular sectors?

Annular sectors are commonly used in engineering, such as in the design of gears, pulleys, and other circular objects. They can also be used to calculate the area of circular gardens or fields in agriculture.

Similar threads

Schools How well does this course prepare me for college math?
    • STEM Academic Advising
Replies
10
Views
4K

Hot Threads

Recent Insights

Back
Top