robinegberts
- 15
- 4
I am asked to solve the differential equation
$$ f''(\eta)+\frac{f'(\eta)}{\eta}+\Big(1-\frac{s^2}{\eta^2}\Big) f(\eta) - f(\eta)^3 = 0, $$
for small ##\eta## and large ##\eta## under the condition ##f(\eta \rightarrow \infty) = 1## and ##f(0)=0##.
The numerically solved solution looks like this:
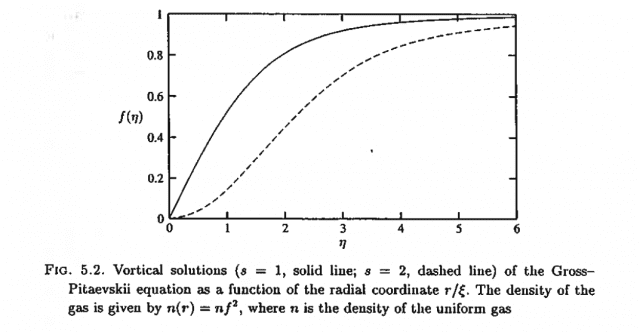
For small ##\eta## clearly ##s^2/\eta^2 \gg 1## and term ##f(\eta)^3 \ll f(\eta)##, which leads to the approximation
$$ f''(\eta)+\frac{f'(\eta)}{\eta}+\frac{s^2}{\eta^2} f(\eta)=0.$$ Is it reasonable to assume ##f''(\eta) \ll f'(\eta)/\eta##? This would lead to the solution solution
$$f'(\eta)=c_1 \eta^{s^2},$$
which shows that for ##s=1## the solution appears to increase linearly for small ##\eta## whereas for ##s=2## the solution appears to increase as ##s^4##.
For large values of ##\eta## one might argue that the differential equation reduces to
$$f''(\eta) + f(\eta) - f(\eta)^3 = 0,$$
however this solution is still unsolvable...
$$ f''(\eta)+\frac{f'(\eta)}{\eta}+\Big(1-\frac{s^2}{\eta^2}\Big) f(\eta) - f(\eta)^3 = 0, $$
for small ##\eta## and large ##\eta## under the condition ##f(\eta \rightarrow \infty) = 1## and ##f(0)=0##.
The numerically solved solution looks like this:
For small ##\eta## clearly ##s^2/\eta^2 \gg 1## and term ##f(\eta)^3 \ll f(\eta)##, which leads to the approximation
$$ f''(\eta)+\frac{f'(\eta)}{\eta}+\frac{s^2}{\eta^2} f(\eta)=0.$$ Is it reasonable to assume ##f''(\eta) \ll f'(\eta)/\eta##? This would lead to the solution solution
$$f'(\eta)=c_1 \eta^{s^2},$$
which shows that for ##s=1## the solution appears to increase linearly for small ##\eta## whereas for ##s=2## the solution appears to increase as ##s^4##.
For large values of ##\eta## one might argue that the differential equation reduces to
$$f''(\eta) + f(\eta) - f(\eta)^3 = 0,$$
however this solution is still unsolvable...