BRS: Conformal Compactifications of Spacetimes. VIII. Plane-Sym Spacetimes (cont'd)
You might have noticed that in the previous post, I was cheating just a bit: I was looking at line elements having the form of a direct product of a two-dimensional Lorentzian manifold (signature -+) with a two-dimensional Riemannian manifold, and I simply ignored the second factor. That makes it much easier to find a transformation bringing the metric of the first factor into a form in which, as expressed in the new chart, the line element is conformal to some simple and familiar manifold.
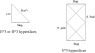
In contrast, recall that in the construction of the standard conformal compactification of Minkowski spacetime in a preceding post in this thread, we found a conformal mapping of Minkowski vacuum into a certain compact region in the Einstein lambdadust, a static spacetime which as a topological manifold is homeomorphic to R \times S^3. Then the fact that the conformal factor blows up on the boundary of this region shows that Minkowski spacetime is inextensible--- it cannot be further extended.
As an example of a more careful construction of a conformal mapping of a plane symmetric spacetime to a region of a spacetime whose causual structure is well understood, specifically the Einstein static lambdadust, let us consider one of the most physically significant of all simple exact solutions of the EFE, the SG16 uniform null dust, which in the Brinkmann chart (1921) is
<br />
\begin{array}{rcl}<br />
ds^2 & = & <br />
-\mu^2 \, (X^2 + Y^2) \, dU^2 - 2 \, dU \, dV + dX^2 + dY^2 \\<br />
&& -\infty < U, \, V, \, X, \, Y < \infty<br />
where \mu is a real constant closely related to the energy density of the wave. Equivalently, the metric tensor can be written as
<br />
g = -\sigma^1 \otimes \sigma^1 <br />
+ \sigma^2 \otimes \sigma^2<br />
+ \sigma^3 \otimes \sigma^3<br />
+ \sigma^4 \otimes \sigma^4<br />
where the Brinkmann coframe field is
<br />
\begin{array}{rcl}<br />
\sigma^1 & =& <br />
\frac{-1}{\sqrt{2}} \; \left( <br />
\left( 1 + q^2 \; (X^2+Y^2)/2 \right) \; dU + dV \right) \\<br />
\sigma^2 & =& <br />
\frac{-1}{\sqrt{2}} \; \left( <br />
\left( 1 - q^2 \; (X^2+Y^2)/2 \right) \; dU - dV \right) \\<br />
\sigma^3 & = & dX \\<br />
\sigma^4 & = & dY<br />
\end{array}<br />
Terminological note: "SG16" refers to the fact that this is the 16th item in the classification by Sippel and Goenner of the possible Lie algebras of Killing vector fields of the pp-wave spacetimes. To avoid possible confusion, I should mention that there are a number of classes of exact waves often encountered in the literature on exact solutions of the EFE. Here is a brief overview:
- Kundt waves are more general than pp-waves; in general they are null dust solutions containing a mixture of gravitational and non-gravitational massless radiation,
- vacuum Kundt waves model purely gravitational waves; they are Petrov type III; the tidal tensor (wrt some family inertial observers) includes "shearing terms" (see D'Inverno's textbook for a sketchy discussion of this),
- in general, a pp-wave has a one-dimensional Lie algebra of Killing vector fields, so that its self-isometry group is a one dimensional Lie group of Lorentzian isometries; the generator of the Lie algebra can be taken to be the wave vector of the wave,
- vacuum pp-waves model purely gravitational waves and are Petrov type N; the tidal tensor (wrt some family of inertial observers) lacks "shearing terms" and has the "spin-two" form (expansion along on direction, contraction along another) which is expected from linearized gtr,
- plane waves are a subclass of pp-waves; their Lie algebra of Killing vector fields is at least five dimensional and the wavefronts are "planar" in the sense that they are homogeneous wrt translations within each wavefront; in general they contain a mixture of gravitational and non-gravitational radiation,
- the vacuum plane waves contain only gravitational radiation; these are the exact solutions corresponding to the linearized approximations studied in almost every gtr textbook in a chapter on linearized gravitational waves.
In more detail: the general pp-wave spacetime is, in the Brinkmann chart,
<br />
\begin{array}{rcl}<br />
ds^2 & = & <br />
-h \, dU^2 - 2 \, dU \, dV + dX^2 + dY^2 \\<br />
&& -\infty < U, \, V, \, X, \, Y < \infty<br />
where h is an arbitrary smooth function of U,X,Y. These will generally be "null dust" solutions which model waves containing a mixture of gravitational and other massless radiation (e.g. EM radiation), with all the radiation sharing the same wave vector \partial_V. The case where h is harmonic in X,Y is exactly the case of the vacuum pp-waves, which contain only gravitational radiation.
For generic h (either general null dust or vacuum case) the only Killing vector field (up to a nonzero constant scalar multiple) is the wave vector field \vec{\xi} = \partial_V, a null geodesic congruence which--- remarkably enough--- is covariantly constant, \nabla_{\vec{Z}} \vec{\xi} = 0 for any vector field \vec{Z}, a property which in fact characterizes the pp-wave spacetimes. But some choices of h give more symmetry. Ehlers and Kundt classified the possible symmetries of vacuum pp-waves, and later Sippel and Goenner did the general case.
The SG16 case is one of the most symmetric of all exact solutions of the EFE: it possesses a seven dimensional Lie algebra of Killing vector fields! Physically, it models a "null dust plane wave" with planar wavefronts and uniform energy density \mu^2/8/\pi. In general, null dust solutions model incoherent massless radiation not having an particular frequency or polarization, but in this case we can if we like add an EM vector potential such that this solution solves both the curved spacetime Maxwell equations and the Einstein equation (this is not possible for the general null dust!). For example
<br />
\vec{A}= -\frac{\mu}{\omega} \, <br />
\cos(\mu \, \omega \, U) \; \partial_X<br />
+ \frac{\mu}{\omega} \, <br />
\sin(\mu \, \omega \, U) \; \partial_Y<br />
gives the exact circularly polarized uniform EM wave in gtr. Alternatively, the exact linearly polarized uniform EM wave is given by the choice of EM potential
<br />
\vec{A} = \mu \, U \; \partial_X<br />
Terminological note: before adding the EM potential, we are dealing with the SG16 null dust, in which the nature of the massless nongravitational radiation is not specified. After adding a suitable EM potential, we are dealing with the SG16 null electrovacuum, modeling either a linearly or circularly polarized uniform EM wave; here "null" means that the principle Lorentz invariants
<br />
F_{ab} \; F^{ab}, \; \; F_{ab} {{}^\ast \!F}^{ab}<br />
of the EM field both vanish identically, as must happen for an EM wave.
Early in the history of gtr, in the special case of plane waves, Rosen found a transformation of a portion of the Brinkmann chart into the so-called Rosen chart, which is much easier to understand. In our example, this transformation is
<br />
\begin{array}{rcl}<br />
u & = & U \\<br />
v & = & V <br />
+ \mu \; \tan(\mu \, U) \; \frac{X^2+Y^2}{2} \\<br />
x & = & X \; \sec(\mu \, U) \\<br />
y & = & Y \; \sec(\mu \, U)<br />
\end{array}<br />
and its inverse transformation is
<br />
\begin{array}{rcl}<br />
U & = & u \\<br />
V & = & v <br />
- \mu \; \sin(\mu \, u) \; \cos(\mu \, u) \; \frac{x^2+y^2}{2} \\<br />
X & = & x \; \cos(\mu \, u) \\<br />
Y & = & y \; \cos(\mu \, u)<br />
\end{array}<br />
Applying this transformation to the SG16 null dust plane wave written in the Brinkmann chart brings the line element into the form
<br />
\begin{array}{rcl}<br />
ds^2 & = & -2 \,du \, dv + \cos(\mu \, u)^2 \; <br />
\left( dx^2 + dy^2) \right) \\<br />
&& -\pi/2 < u < \pi/2, \; \; -\infty < v, \, x, \, y < \infty<br />
\end{array}<br />
This has a nice "fringe benefit": the obvious frame field read off the line element is not the original frame field but a new one, the Rosen frame field
<br />
\begin{array}{rcl}<br />
\vec{e}_1 & = & \frac{1}{\sqrt{2}} \; <br />
\left( \partial_u + \partial_v \right) \\<br />
\vec{e}_2 & = & \frac{1}{\sqrt{2}} \; <br />
\left( -\partial_u + \partial_v \right) \\<br />
\vec{e}_3 & = & \frac{1}{\cos(\mu \, u)} \; \partial_x \\<br />
\vec{e}_4 & = & \frac{1}{\cos(\mu \, u)} \; \partial_y<br />
\end{array}<br />
which is
inertial nonspinning.
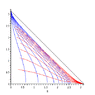
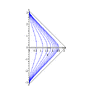
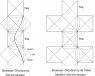
The Rosen chart covers only the region \frac{-\pi}{2 \mu} < u < \frac{\pi}{2 \mu}, which corresponds to the "strip" \frac{-\pi}{2 \mu} < U < \frac{\pi}{2 \mu} in the Brinkmann chart, because of the rather obvious coordinate singularities in the Rosen chart. These have a physical significance: the Rosen observers in a given x,y plane initially isotropically expand, then momentarily "hover", then isotropically contract and form a "caustic" where they momentarily "occupy the same point", so to speak, and where the expansion tensor of the congruence blows up. (As with expansion in FRW models, the caustic does not have a particular location in the x,y plane.) Then the expansion/recontraction cycle repeats, but only one cycle is covered by each Rosen chart.
The "physical reason" for the repeated expansion/recontraction cycles experienced by our family of Rosen observers (recall that they are inertial observers, so no non-gravitational forces act on them) is of course the fact that the EM wave carries mass-energy, and this energy attracts test particles.
Thus, the strip -\pi/2 < U < \pi/2 in the Brinkmann chart has a particular physical significance in terms of the Rosen congruence. (As you might have noticed, strictly speaking there are infinitely many Rosen congruences in our SG16 spacetime related by "phase shifts".)
Similar remarks hold, incidently for other plane waves. In particular, the vacuum plane waves include the exact monochromatic gravitational plane wave (the exact solution whose linearized approximation is studied in most gtr textbooks), and in this solution, there is a congruence of Rosen observers who also periodically expand and contract, with the difference that they form geometrically different caustics.
(Since I have previously discussed this in great detail, to avoid possible confusion, I should say that from the point of view of a family of Rosen observers,
- in a model of a uniform EM wave (linearly or circularly polarized wave, SG16 in the classification of Sippel and Goener), the observers in each x,y plane periodically converge isotropically, meet in a "point caustic", then begin a new expansion/recontraction cycle,
- in a model of a uniform linearly polarized gravitational wave (EK11_0 in a suitable extension of the classification of Ehlers and Kundt, which didn't specifically identify all cases), the observers in an x,y plane expand along one direct but periodically converge anisotropically along another, so they periodically meet along a "line caustic", then begin a new expansion/recontraction cycle,
- in a model of a circularly polarized gravitational wave (EK11), well, here I'll just say that's a different case.
Here "point, line" refer temporarily to the picture in "space at a time" (permissible in the first two cases because the congruence of Rosen observers is vorticity-free. In the second case, the "physical reason" for the repeated expansion/recontraction cycles experienced by the Rosen observers is of course the fact that--- although the stress-energy tensor does not account for this!--- the gravitational wave carries energy and this energy attracts test particles. Compare the discussion in MTW of the "background" of a closely related gravitational plane wave.)
Another remarkable property of the SG16 plane wave is that it is a conformally flat spacetime. We know that because its Weyl tensor vanishes identically. (In contrast, the generic pp-wave is Petrov type N.) The property of conformal flatness characterizes the pp-waves which contain no gravitational radiation, incidentally. This property implies that there must a coordinate transformation such that the line element written in the new chart has the factor of a nonzero scalar function (the conformal factor) times a line element we can recognize as the line element of Minkowski spacetime written in some chart.
What might this transformation be? Well, Maldacena noticed (c. 2002) that a transformation which is quite similar to Rosen's transformation does the trick, namely:
<br />
\begin{array}{rcl}<br />
u & = & \tan(\mu \,U) \\<br />
v & = & V + \mu \, \tan(\mu \, U) \; \frac{X^2+Y^2}{2} \\<br />
x & = & \sqrt{\mu} \, X \, \sec(\mu \, U) \\<br />
y & = & \sqrt{\mu} \, Y \, \sec(\mu \, U)<br />
\end{array}<br />
whose inverse transformation is
<br />
\begin{array}{rcl}<br />
U & = & \frac{1}{\mu} \; \operatorname{arctan}(u) \\<br />
V & = & v - \frac{u}{1+u^2} \; \frac{x^2+y^2}{2} \\<br />
X & = & \frac{1}{\sqrt{\mu}} \; \frac{x}{1+u^2} \\<br />
Y & = & \frac{1}{\sqrt{\mu}} \; \frac{y}{1+u^2}<br />
\end{array}<br />
when applied to the SG16 plane wave written in the Brinkmann chart brings the "strip" -\pi/2 < U < \pi/2 to
<br />
\begin{array}{rcl}<br />
ds^2 & = & \frac{1}{\mu \,(1+u^2)} \; \left( - 2 \, du \, dv<br />
+ dx^2 + dy^2 \right) \\<br />
&& -\infty < u, \, v, \, x, \, y < \infty<br />
\end{array}<br />
Thus, the null geodesics in the "strip" behave just like null geodesics in the
entire Minkowski spacetime.
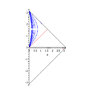
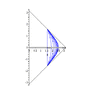
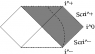
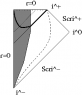
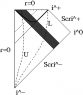
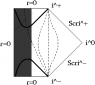
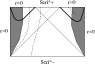
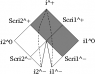
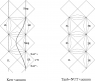
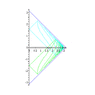
Now we can conformally map the entire Minkowski spacetime to a diamond-shaped region on the Einstein static lambdadust, corresponding the strip -\pi/2/\mu < U < \pi/2/\mu[/tex] in the Brinkmann chart. The combined conformal factor blows up on only part of the previous boundary, so if we didn't already know that we can analytically extend the strip, this procedure would have told us that fact. Carrying out the extension in the Einstein static lambdadust, we find that the SG16 uniform conformally flat null dust plane wave is conformal to the entire Einstein static lambdadust with one null curve removed. This appears as a helical curve in the usual depiction of the Einstein static lambdadust with two angular coordinates suppressed as a "cylinder" (see Hawking and Ellis, <i>Large Scale Structure of Space-Time</i>, Cambridge University Press, 1972 for the three dimensional depiction I have in mind, from which it should be obvious which helical curve I have in mind). Every "point" in the diagram represents a round Riemannian two-sphere, <i>except</i> for points on this helical curve, which represent points. See the figure below. (Berenstein and Nastase, hep-th/0205048, offer a badly drawn picture of this null curve drawn on the cylinder; I think it may be clearer to "unwrap" the cylinder as shown in the figure below.) In other words, in this sense, the conformal boundary of the SG16 conformally flat uniform energy density null dust plane wave is one dimensional.<br />
<br />
Maldacena's transformation, like Rosen's transformation, has a nice fringe benefit: there is an obvious frame field which we can read off the line element written in the Maldacena chart. Transforming this frame back to the Brinkmann chart, we can write three frame fields in terms of the Brinkmann chart: the original Brinkmann frame, the Rosen frame, and the Maldacena frame. As we saw, the Rosen frame models certain nonspinning inertial observers who experience repeated expansion/recontraction cycles, with this relative motion occurring within planes, and with one cycle just fitting in the strip -\pi/2/\mu &lt; U &lt; \pi/2/\mu; in the Brinkmann chart we can "see" these cycles and the resulting caustics. In contrast, the Maldacena frame models certain noninertial observers who experience <i>isotropic</i> expansion and recollapse, with the relative motion being three-dimensional, and whose <i>entire history</i> fits in -\pi/2/\mu &lt; U &lt; \pi/2/\mu. What is more, all the fields (i.e. the EM field and the Riemann curvature components) tend to zero, as measured by the Maldacena observers, as they approach future conformal infinity. However, their spatial hyperslices are asymptotic to H^3 in this limit.<br />
<br />
We have mapped our SG16 solution--- recall this includes the exact uniform EM wave (either linearly or circularly polarized)--- to a <i>non</i>-compact region of the Einstein static lambdadust, so strictly speaking, "conformal compactification" is a misnomer in this case. In any case, the important point here is that the SG16 null dust plane wave lacks any asympotically flat sheet, so we should not be very surprised that its conformal structure turns out to be quite unlike that of Minkowski spacetime. In particular, the "locus at conformal infinity" is two-dimensional for the Minkowski spacetime (and asympototically flat sheets in other spacetimes), but one-dimensional for the SG16 conformally flat uniform energy density plane wave.<br />
<br />
It is instructive to briefly review "three levels of accuracy" in gtr in modeling uniform EM waves (linearly or circularly polarized):<br />
<ul>
<li data-xf-list-type="ul"> "test field": ignore all gravitational effects entirely and work in Minkowski vacuum; then each integral curve of the wave vector field "begins" at some point on a <i>three dimensional</i> locus ("past conformal infinity", or scri^- in the standard Penrose diagram for Minkowksi vacuum) and "ends" at some point on another three dimensional locus ("future conformal infinity", or scri^+ in the standard Penrose diagram),</li>
<li data-xf-list-type="ul"> "linearized gtr": ignore all second order gravitational effects; the linearized uniform EM wave solution suggests that inertial observers (Rosen observers) will contract isotropically in the x,y plane due to the gravitational attraction of the energy in the wave, but cannot give the correct global conformal structure,</li>
<li data-xf-list-type="ul"> the exact uniform EM wave (the SG16 null dust made into a null electrovacuum by adding a suitable EM potential): fully accounts for both EM and gravitational effects, and turns out to have a conformal structure quite different from that of more naive models; each integral curve of the wave vector field begins on a <i>one-dimensional</i> locus ("past conformal infinity") and ends a a point on "another" one-dimensional locus ("future conformal infinity").</li>
</ul>Put more pointedly: the global conformal structure of the exact solution, null geodesics issue from a <i>one-dimensional</i> locus of possible "directions plus emission 'times' at past conformal infinity", rather than from a <i>three-dimensional</i> locus of possible "directions plus emission 'times' at past conformal infinity".<br />
<br />
In the latter case, we can think of "the sphere at conformal past infinity" persisting over time. In the former case, due to the isotropic nature of the expansion/recontraction cycles noted above, we can say that it is impossible (in the SG16 null dust) to identify a particular "direction at conformal past infinity" from which a given null geodesic "originated".<br />
<br />
By now, I hope the reader is eager to compare the above discussion with the case of a linearly polarized uniform gravitational wave. Maybe you can guess the dimension of the locus at "conformal infinity"!<br />
<br />
Figure:<br />
<ul>
<li data-xf-list-type="ul"> Left: the "strip" -\pi/2/\mu &lt; U &lt; \pi/2/\mu conformally mapped into a "diamond" shaped region in the Einstein static lambdadust; inside the "diamond", the wave vector field goes from lower right to upper left as indicated. </li>
<li data-xf-list-type="ul"> Right: Rosen observers experience repeated expansion-contraction cycles; I have also sketched (bold) a typical timelike curve, i.e. world line of a typical observer. I recommend thinking of this picture as "the Penrose diagram of the uniform EM wave" (even though this misses some important features); points on the boundary represent points, and points in the interior represent round Riemannian two-spheres having some radius. In contrast, in the Penrose diagram for Minkowski vacuum, points on scri^+ or scri^- represent round two-spheres corresponding to the possible directions.</li>
</ul>
Fortunately, along comes a little entertainment, a collapsing spherical shell of massless radiation which focuses on the locus r=0. As the shell passes, our observer measures tidal forces and after a while finds he is outside a newly formed black hole. But now consider the dashed curve labeled U (for "unlucky"), which denotes the world line of an observer who happens to be a bit closer to r=0. He too initially believes he is living in Minkowski vacuum, and r=0 is not even a distinguished place yet. Bye and bye along comes the collapsing spherical shell. After a short time our observer finds he is outside a massive object and falling inwards (decreasing r), and to his horror, he finds he is unable to escape. Shortly later, his world line approaches the strong spacelike curvature singularity in his immediate future and he meets his gruesome demise.
