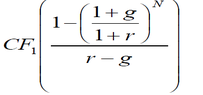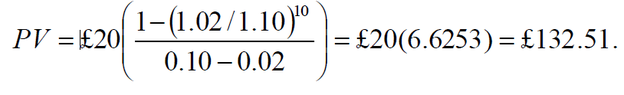Calculate Present Value of 10-Year Lease w/ OCC & Variable Rental

In summary, the conversation is about finding the present value of a 10-year lease with increasing rent payments and a 10% annual interest rate. The correct answer is £132.51, but the person initially got a wrong answer of -23.88 due to using incorrect data in their calculator. They were able to solve the problem with the correct data and thanked everyone for their help.
  • #1
logicandtruth
11
0
Hi all

Trying to improve my level of maths and would like some help with the below question please.

A 10-year lease with annual rental payments to be made at the end of each year, with the rent increasing by 2% each year. If the first year rent is £20 and the OCC is 10% per year, what is the Present value of the lease?

The formula for present value of a level annuities is below (for a growing interest rate)

View attachment 8227

According to my book the answer should be £132.51, but I get -23.88.

View attachment 8228

Could anyone tell me where I am misinterpreting the formula?
 

Attachments

  • PV Formula.PNG
    PV Formula.PNG
    2.5 KB · Views: 69
  • PV Formula Answer.PNG
    PV Formula Answer.PNG
    4.7 KB · Views: 56
Mathematics news on Phys.org
  • #2
Book is correct. Are you using a calculator?
You're probably entering the data wrongly...we can't tell...
Try it this way:
u = (1.02/1.10)^10
v = .10 - .02

PV = 20*(1 - u) / v
 
  • #3
Yes it works I must have been using the incorrect figure with my calculator.

Many thanks
 

1. What is the formula for calculating present value?

The formula for calculating the present value of a 10-year lease with an occupancy cost and variable rental is: PV = (R x (1- (1 + i)^-n))/i, where R is the annual rental amount, i is the discount rate, and n is the number of years.

2. How do I determine the occupancy cost and variable rental for the calculation?

The occupancy cost is the fixed amount that the tenant must pay each year for the lease. The variable rental is the additional amount that may be charged based on certain conditions, such as changes in market rates or performance of the property. These amounts should be specified in the lease agreement.

3. What is the discount rate and how do I determine it?

The discount rate is the rate at which future cash flows are discounted to their present value. It takes into account the time value of money and the risk associated with the investment. The discount rate can be determined by considering factors such as the current interest rates, inflation, and the specific risk of the investment.

4. Can the present value of a 10-year lease change over time?

Yes, the present value of a 10-year lease can change over time. This is because it is affected by factors such as changes in the occupancy cost, variable rental, and discount rate. Additionally, changes in the real estate market or the performance of the property can also impact the present value.

5. How can I use the present value calculation for decision-making?

The present value calculation can help you make informed decisions about whether to enter into a 10-year lease with an occupancy cost and variable rental. It can also be used to compare the present value of different lease options or to determine the maximum amount that should be paid for a lease in order to achieve a desired rate of return.

Similar threads

MHB Equivalent Rates - Valuation Mathematics
    • General Math
Replies
2
Views
2K
Calculate PV for Annuity Problem w/ 5.5% Discount Rate ($50K/yr Payments)
    • Precalculus Mathematics Homework Help
Replies
10
Views
5K
MHB Calculating the Payout Ratio: How Investors Value Alibaba's IPO
    • General Math
Replies
1
Views
3K
Basic finance Present Value and Anuity
    • Calculus and Beyond Homework Help
Replies
5
Views
2K
How Much Will Mike Save by Age 60 With a Growing Salary and Fixed Savings Rate?
    • Precalculus Mathematics Homework Help
Replies
3
Views
4K
Student Loan Payment Calculation and Effective Interest Rate Analysis
    • Precalculus Mathematics Homework Help
Replies
14
Views
7K
Calculating Present Value of a Growing Annuity with Monthly Payments
    • Calculus and Beyond Homework Help
Replies
4
Views
2K
B Chi-squared test stat choosing a critical value
    • Set Theory, Logic, Probability, Statistics
Replies
5
Views
2K
Problem about Financial Planning
    • Precalculus Mathematics Homework Help
Replies
16
Views
4K
Solved: Calculator Issues? Annuity Value at 6 Years w/ 6.8% Compounded Annually
    • Precalculus Mathematics Homework Help
Replies
8
Views
2K

Hot Threads

Recent Insights

Back
Top