Calculate the tension in the rope

[MathewsMD]

If the gymnast has a mass, m = 36.7 kg, and the angle θ = 4.0°, calculate the tension in the rope from which she is hanging.

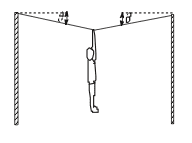
ƩF_x = T_1x - T_2x = 0
Then T₁cos4 = T₂cos4
T₁ = T₂ = T

ƩF_y = 2T_y - mg
2Tsin4 = mg
T = mg/2sin4 = 2578 N

I have gotten the solution. I am just confused at one part. Do we analyze the tension in the string on each side of the gymnast separately, then add them together? Or, do we just find the tension on one side and that is it (like my solution)?

I am just confused since I remember learning tension in a massless rope is considered to be uniform, but if there is a force being applied to a part of it (this time in the middle) I don't know if we're supposed to analyze tension together or not since it is essentially a node and I considered it like I would two separate strings in my solution.

Also, if the gymnast was not in the middle of the string (i.e. θ₁ = 6.0° and θ₂ = 10.0°) how would this change the situation and the resultant tension in the rope. Would it have any effect?

Any help would be greatly appreciated!

 

[Nugatory]

You are right to treat it as two separate strings, for exactly the reason that you said: you can treat any point in the rope as a node and require that the forces on it all cancel (as long as the rope isn't accelerating, of course).

If you change the angles, then it becomes even more important to think about it this way, because in general the tension in the two sides will be different. That sounds like a violation of the rule that the tension is uniform throughout the rope, but it's not. The only way of getting different angles is to physically hook the gymnast to a particular point on the rope, and then you really have two separate ropes connected to the eye of the hook, each with their own tension.

(If you don't have that fixed hook, the gymnast's attachment point will slide down the rope until we reach equilibrium with the tensions and angles equal).

 

[MathewsMD]

You are right to treat it as two separate strings, for exactly the reason that you said: you can treat any point in the rope as a node and require that the forces on it all cancel (as long as the rope isn't accelerating, of course).

If you change the angles, then it becomes even more important to think about it this way, because in general the tension in the two sides will be different. That sounds like a violation of the rule that the tension is uniform throughout the rope, but it's not. The only way of getting different angles is to physically hook the gymnast to a particular point on the rope, and then you really have two separate ropes connected to the eye of the hook, each with their own tension.

(If you don't have that fixed hook, the gymnast's attachment point will slide down the rope until we reach equilibrium with the tensions and angles equal).

Thank you!