Calculate Volume of Truncated Square Pyramid | Yahoo Answers

[MarkFL]

Here is the question:

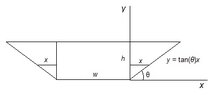
Truncated Pyramid Question?

If the angle of repose is given as 32 degrees, the height is 18cm and the top square is 20*20cm, can I calculate the volume?

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Sam G,

One method we can use to calculate the volume of the pyramid is to use a technique from integral calculus called volumes by slicing. We will slice the pyramid into horizontal square slices and then add the slices by integrating.

I would choose to orient the cross-section of the pyramid as follows:

View attachment 1132

We can now see that the volume of an arbitrary slice, a square slice of side length $s$ and thickness $dy$ is:

\(\displaystyle dV=s^2\,dy\)

where:

\(\displaystyle s=w+2x=w+2\cot(\theta)y\)

and so we have:

\(\displaystyle dV=\left(w+2\cot(\theta)y \right)^2\,dy= \left(w^2+4w\cot(\theta)y+4\cot^2(\theta)y^2 \right)\,dy\)

Now, summing the slices by integration, we find:

\(\displaystyle V=\int_0^h w^2+4w\cot(\theta)y+4\cot^2(\theta)y^2\,dy\)

Applying the FTOC, we obtain:

\(\displaystyle V=\left[w^2y+2w\cot(\theta)y^2+\frac{4}{3}\cot^2(\theta)y^3 \right]_0^h=w^2h+2w\cot(\theta)h^2+\frac{4}{3}\cot^2( \theta)h^3\)

\(\displaystyle V=\frac{h}{3}\left(4\cot^2( \theta)h^2+6w\cot(\theta)h+3w^2 \right)\)

Using the given data:

\(\displaystyle h=18\text{ cm},\,w=20\text{ cm},\,\theta=32^{\circ}\)

we find:

\(\displaystyle V\approx47855.220519615943\text{ cm}^3\)