Buzz Bloom
Gold Member
- 2,517
- 465
- TL;DR
- I used a spreadsheet (PNG image in main body section) to analyze 12 values with +/- error ranges which I assume for the purpose of this calculation to be standard deviation values. I am seeking conformation or corrections regarding the validity of the method I used.
Below is the spreadsheet image.
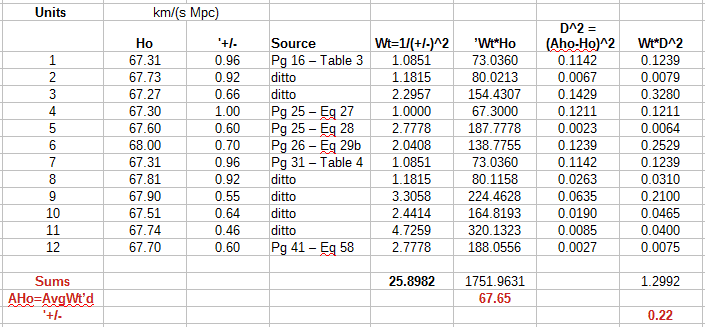
The source of the data in the two columns, Ho and +/-, is the following article
The Ho column contains the 12 values, Hi, for the Ho variable, i being the index (of a variable value) ranging from 1 to 12.
The +/- column contains for each Hi value the corresponding value of an error range, Ei, which I assume to be of 1 standard deviation σi.
The Source column specifies where in the article the particular 12 values for Hi and Ei are found.
The Wt=... column contains values, Wi, for the weights for calculating weighted sums. I assume that the appropriate choice of weight are the squares of the reciprocals of the Ei values.
The Wt*Ho column contains weighted Ho values
I feel confident that this result is OK for AH. I am less confident that my calculation below of AE is OK. I will present my analysis, and explain my main concern about AE, in what follows.
The D2^2=... column contains values, D2i, of the squares of the 12 differences between AH and a value of Ho.
I now define Aσ as square root of a quotient: the weighted sum of squared differences and the sum of weights. Using [3] and [10]

I do not know how to adjust this for weighted samples.
Another minor concern is that my assumtion to use 1/Ei2 as weights may not be the right approach. However, I think I have a good rational for doing this, but it is rather complicated, so I will not include it in this post. If anyone would like to see this rationale, I will post it later.
The source of the data in the two columns, Ho and +/-, is the following article
Let AHo be the conjoined weighted average values for Ho and the corresponding error ranges.[1] AHo = AH +/- AE = 67.65 +/- 0.22.
The Ho column contains the 12 values, Hi, for the Ho variable, i being the index (of a variable value) ranging from 1 to 12.
The +/- column contains for each Hi value the corresponding value of an error range, Ei, which I assume to be of 1 standard deviation σi.
The Source column specifies where in the article the particular 12 values for Hi and Ei are found.
The Wt=... column contains values, Wi, for the weights for calculating weighted sums. I assume that the appropriate choice of weight are the squares of the reciprocals of the Ei values.
[2] Wi = 1/Ei2
The sum of this column is[3] ΣW = Σ[i=1 to 12] Wi = 25.8982 .
The Wt*Ho column contains weighted Ho values
[4] WHi = Wi Hi.
The sum of this column is[5] ΣWH = Σ[i=1 to 12] WHi = 1751.9631 .
The weighted average, AH, is[6] AH = ΣWH / ΣW = 67.65.
I feel confident that this result is OK for AH. I am less confident that my calculation below of AE is OK. I will present my analysis, and explain my main concern about AE, in what follows.
The D2^2=... column contains values, D2i, of the squares of the 12 differences between AH and a value of Ho.
[7] D2i = (Ho-Hi)2
Althought not part of the calculations, it will later be useful to also have defined the sum of the differences squared.[8] ΣD2 = Σ[i=1 to 12] (D2i)
The Wt*D2 column contains values, WD2i, of the product of a weight and a squared difference.
[9] WD2i = Wi D2i
[10] ΣWD2 = Σ[i=1 to 12] (WD2i) = 1.2992
I now define Aσ as square root of a quotient: the weighted sum of squared differences and the sum of weights. Using [3] and [10]
[11] Aσ = (WD2/ΣW)1/2 = 1.2992/25.8982 = 0.22
The main reason I am uncertain is that if all of the Ei values were the same, say 1/s, then then the sum of the weights, ΣW, would be[12] ΣW = (12/s)2.
Then the sum of the weighted squares of differences, ΣWD, would be[`13] ΣWD2 = (1/s2) Σ[i=1 to 12] (D2i)
= (1/s)2)ΣD2
and Aσ would be[14] Aσ = [(1/12)ΣD2]1/21/2.
Ordinarily, since there are 12 samples I would expect[15] Aσ = [(1/11) ΣD2]1/21/2.
Equation [15] is based on the articleI do not know how to adjust this for weighted samples.
Another minor concern is that my assumtion to use 1/Ei2 as weights may not be the right approach. However, I think I have a good rational for doing this, but it is rather complicated, so I will not include it in this post. If anyone would like to see this rationale, I will post it later.
Last edited: