Calculating Exponents for Business Model

In summary, the conversation discusses a math problem involving exponents and using a spreadsheet to solve it. The person is looking for a way to simplify the calculations into one formula rather than having to calculate each one independently. They suggest using a capable calculator or researching how to evaluate a function with multiple inputs on one spreadsheet. The expert suggests using the general formula of 280*.985^n to find each value. The person asks for clarification on what the expert is looking for.
  • #1
DesperatelyLost
2
0
Hi, Everyone.

I suspect I am a bit unique here. I'm struggling with a math problem for a business model rather than a homework assignment. It's been quite a while since I have worked with exponents and I am hoping someone can assist me with a question.

I have the following calculations:
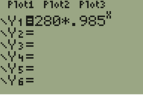
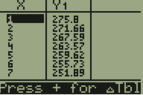
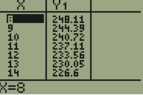
280*.985^11
280*.985^10
280*.985^9
280*.985^8
280*.985^7
280*.985^6
280*.985^5
280*.985^4
280*.985^3
280*.985^2
280*.985^1

The base and coefficient are the same, but the exponent is not. I know that I can't add the exponents because they are not like terms. Is there a way to simplify this into one formula or do I need to calculate each one independently?

Thank you in advance for your assistance!
 
Mathematics news on Phys.org
  • #2
use a capable calculator or a spreadsheet ...
 

Attachments

  • expfunction.png
    expfunction.png
    432 bytes · Views: 85
  • exp_table1.png
    exp_table1.png
    620 bytes · Views: 80
  • exp_table2.png
    exp_table2.png
    551 bytes · Views: 78
  • #3
I'm already using a spreadsheet, but it's cumbersome to write out that large of a formula.
 
  • #4
DesperatelyLost said:
I'm already using a spreadsheet, but it's cumbersome to write out that large of a formula.

I'm not a spreadsheet expert, so you'll probably need to research how to evaluate a function with multiple inputs on one ... or wait until someone with the necessary expertise posts a reply.
 
  • #5
"280*.985^11
280*.985^10
280*.985^9
280*.985^8
280*.985^7
280*.985^6"

Cell A1: Enter 280
Cell A2: Enter 0.985
Cell A3: Enter 0
Cell A4: Enter =A3+1
Cells A5-A100: Copy the contents of A4 and paste
Cell B3: =A[dollar sign]1*A[dollar sign]2^A3
Cells B4-B100: Copy the contents of B3 and paste

It's upside down from your design, but small changes will solve that problem.
 
  • #6
I'm not sure what you are looking for.
The general formula is 280*.985^n.
Each next value can be found by multiplying the previous value by .985,
Or alternatively each value can be found by the general formula.
Can you clarify what you are looking for?
 

FAQ: Calculating Exponents for Business Model

How do I calculate exponents for my business model?

To calculate exponents for your business model, you will need to use the exponent rule, which states that when multiplying powers with the same base, you add the exponents. For example, if your business model has a base of 2 and an exponent of 3, and you need to multiply it by 2 with an exponent of 4, the calculation would be 2^3 x 2^4 = 2^(3+4) = 2^7. This would give you the final exponent for your business model.

Why is it important to calculate exponents for my business model?

Calculating exponents for your business model is important because it allows you to understand the growth potential and scalability of your business. Exponents represent repeated multiplication, so a higher exponent means a faster rate of growth. This can help you make informed decisions about investments, pricing, and future projections for your business.

What is the difference between a positive and negative exponent in a business model?

A positive exponent in a business model represents growth or increase, while a negative exponent represents a decrease or decline. For example, a positive exponent of 2 would mean your business is growing at a rate of 2 times, while a negative exponent of 2 would mean your business is declining at a rate of 2 times.

Can I use exponents to predict future growth for my business?

Yes, exponents can be used to predict future growth for your business. By analyzing the current exponent of your business model and making projections based on market trends and potential investments, you can estimate the potential growth of your business in the future.

How can I use exponents to compare different business models?

Exponents can be used to compare different business models by looking at the growth rates represented by their exponents. A higher exponent would indicate a faster rate of growth, while a lower exponent would indicate a slower rate of growth. This can help you determine which business model has a higher potential for success and profitability.

Similar threads

Calculating tq for incline / best practices for gear reduction
Replies
7
Views
2K
MHB Correlation to Winning question
Replies
2
Views
2K
I Modeling Asteroid Rotation Using Quaternions: Seeking Guidance on Init
Replies
3
Views
1K
MHB How Many Iterations Can Be Expected from Drawing Cards in Better Backstories?
Replies
1
Views
922
MHB Did I Simplify These Precalculus Problems Correctly?
Replies
1
Views
2K
MHB Which Catering Service Maximizes Charity Profit for a Business Banquet?
Replies
2
Views
6K
MHB Adding in Base 20: 1HE1C +JDF0 = 2H7GC
Replies
4
Views
2K
MHB How do I calculate the side of a rhombus using the bisector of an angle theorem?
Replies
1
Views
2K
MHB What is a Prize Payout Calculator and How Can It Help with Variable Inputs?
Replies
8
Views
12K
MHB Free Math Tutoring Videos Focusing on Math Olympiad, Calculus, and High School Math
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top