Calculating Tension in a Model Plane's Horizontal Circular Motion

[st3dent]

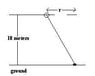
A model plane of mass .75 kg is flying at a constant speed in a horizontal circle connected to a 30 m cord and is at a height of 18 m. The other end of the cord is tethered to the ground as shown in the picture. The plane makes 4.4 revolutions per minute, and the force that the air exerts on the plane is perpendicular to the wings. What is the tension in the cord?


I can see that the ball moves in constant circular motion with r as its radius.

I know that since the ball makes 4.4 revolutions/minute means that the ball has a period(T) of 13.63 seconds.

I also realize that the sum of all forces = ma
As F = ma, Gm₁m₂/ r² = ((m)(4 pi²)(r)) / T²

I see that the force of tension (F_t) has an upwards component of F_tsinx that balances the downwards mg and a left component of F_tcosx that directly causes the circular motion.

However, I do not know how to approach this problem.
Where do I start...your help is much appreciated.

 

[swansont]

Any object moving in a circle at constant speed must feel a force of mv²/r toward the center. In this case, what could be supplying that force?

 

[st3dent]

Gravity...but how do I solve this damn problem?

 

[Doc Al]

Gravity...but how do I solve this damn problem?

Use Newton's 2nd law! First identify all the forces on the plane. Then realize that the acceleration is centripetal, as swansont explained. Hint: the air pushes up (and back) on the plane, gravity pulls down... what is pulling it toward the center?

 

[HallsofIvy]

Gravity...but how do I solve this damn problem?

NO! Gravity pulls downward. The plane is not going downward, it is going in a horizontal circle. What is keeping the plane in that circle?