Pull and Twist
- 48
- 0
Hey all, I'm currently working a Calculus problem that requires me to sketch $$f(x)=(3x-1)/(x-1)^2$$ without using a calculator.
Part A: Requires that we find;
i. x-intercept:
$$f(0)=(3*0-1)/(0-1)^2=-1$$
So $$f(0)=-1$$
ii. y-intercept:
$$f(x)=0$$ therefore; $$3x-1=0$$ or $$x=1/3$$
So $$f(1/3)=0$$
iii. horizontal asymptote:
This is where I get stuck...
My initial thought is to use limits of x as it approaches $$\infty$$.
$$\lim_{{x}\to{\infty}}f(x)=(3x-1)/(x-1)^2$$
$$\lim_{{x}\to{\infty}}f(x)=(3x-1)/(x^2-2x+1)$$
$$\lim_{{x}\to{\infty}}f(x)=(3/x-1/x^2)/(1-2/x+1/x^2)$$
$$f(x)=(3/\infty-1/\infty^2)/(1-2/\infty+1/\infty^2)$$
$$f(x)=(0-0)/(1-0+0)=0$$
So the horizontal asymptote is at y=0 when we approach $$\infty$$??
Also, if I then take $$\lim_{{x}\to{-\infty}}$$ of the function I would also get 0??
iii. vertical asymptote:
$$f(x)=(3x-1)/(x-1)^2$$
$$(x-1)^2=0$$
$$x=1$$
So then the vertical asymptote is at $$x=1$$?
Part B: Find the intervals of increase and decrease, and the local and maximum and minimum values.
$$f(x)=(3x-1)/(x-1)^2$$
$$f'(x)=((x-1)^2(3)-(3x-1)(2(x-1)*(1)))/((x-1)^2)^2$$
$$f'(x)=((3(x-1)^2)-(2(3x-1)(x-1)))/(x-1)^3$$
$$f'(x)=(3x-3-6x+2)/(x-1)^3$$
$$f'(x)=(-3x-1)/(x-1)^3$$
So then we can solve for the Critical Points:
We know $$x\ne1 $$and $$-3x-1=0 \implies x=-1/3$$
If we then take $$f(-1/3)=(3x-1)/(x-1)^2$$ we get $$f(-1/3)=-9/8$$
So our intervals are $$(-\infty,-1/3),(-1/3,1),(1,\infty)$$
[table="width: 500, class: grid"]
[tr]
[td][/td]
[td]$$-3x-1$$[/td]
[td]$$x-1$$[/td]
[td]$$f'(x)$$[/td]
[/tr]
[tr]
[td]$$(-\infty,-1/3)$$[/td]
[td]$$+$$[/td]
[td]$$-$$[/td]
[td]decreasing[/td]
[/tr]
[tr]
[td]$$(-1/3,1)$$[/td]
[td]$$-$$[/td]
[td]$$-$$[/td]
[td]increasing[/td]
[/tr]
[tr]
[td]$$(1,\infty)$$[/td]
[td]$$-$$[/td]
[td]$$+$$[/td]
[td]decreasing[/td]
[/tr]
[/table]
Based on the table, we can tell which intervals are increasing and decreasing and that the local minimum is $$f(-1/3)=-9/8$$ and since we have a vertical asymptote at 1, there is no local max.
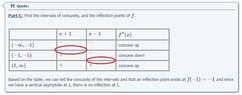
Part C: Find the intervals of concavity, and the inflection points of $$f$$.
$$f'(x)=(-3x-1)/(x-1)^3$$
$$f''(x)=(((x-1)^3)(-3)-(-3x-1)(3(x-1)^2*(1)))/((x-1)^3)^2$$
$$f''(x)=((-3(x-1)^3)-3(x-1)^2(-3x-1)/(x-1)^6$$
$$f''(x)=(-3(x-1)^2((x-1)+(-3x-1)))/(x-1)^6$$
$$f''(x)=(-3(-2x-2))/(x-1)^4$$
$$f''(x)=(6(x+1))/(x-1)^4$$
So then we can solve for the Critical Points:
We know $$x\ne1 $$and $$x+1=0 \implies x=-1$$
If we then take $$f(-1)=(3x-1)/(x-1)^2$$ we get $$f(-1)=-1$$
So our intervals are $$(-\infty,-1),(-1,1),(1,\infty)$$
[table="width: 500, class: grid"]
[tr]
[td][/td]
[td]$$x+1$$[/td]
[td]$$x-1$$[/td]
[td]$$f''(x)$$[/td]
[/tr]
[tr]
[td]$$(-\infty,-1)$$[/td]
[td]$$-$$[/td]
[td]$$-$$[/td]
[td]concave up[/td]
[/tr]
[tr]
[td]$$(-1,1)$$[/td]
[td]$$+$$[/td]
[td]$$-$$[/td]
[td]concave down[/td]
[/tr]
[tr]
[td]$$(1,\infty)$$[/td]
[td]$$+$$[/td]
[td]$$+$$[/td]
[td]concave up[/td]
[/tr]
[/table]
Based on the table, we can tell the concavity of the intervals and that an inflection point exists at $$f(-1)=-1$$ and since we have a vertical asymptote at 1, there is no inflection at 1.
Part D: Combine all the information from Part A-C and sketch the function.
I am currently working on this part and will post it once I am done.
Will someone let me know if I approaching this correctly?? Thank you.
Part A: Requires that we find;
i. x-intercept:
$$f(0)=(3*0-1)/(0-1)^2=-1$$
So $$f(0)=-1$$
ii. y-intercept:
$$f(x)=0$$ therefore; $$3x-1=0$$ or $$x=1/3$$
So $$f(1/3)=0$$
iii. horizontal asymptote:
This is where I get stuck...
My initial thought is to use limits of x as it approaches $$\infty$$.
$$\lim_{{x}\to{\infty}}f(x)=(3x-1)/(x-1)^2$$
$$\lim_{{x}\to{\infty}}f(x)=(3x-1)/(x^2-2x+1)$$
$$\lim_{{x}\to{\infty}}f(x)=(3/x-1/x^2)/(1-2/x+1/x^2)$$
$$f(x)=(3/\infty-1/\infty^2)/(1-2/\infty+1/\infty^2)$$
$$f(x)=(0-0)/(1-0+0)=0$$
So the horizontal asymptote is at y=0 when we approach $$\infty$$??
Also, if I then take $$\lim_{{x}\to{-\infty}}$$ of the function I would also get 0??
iii. vertical asymptote:
$$f(x)=(3x-1)/(x-1)^2$$
$$(x-1)^2=0$$
$$x=1$$
So then the vertical asymptote is at $$x=1$$?
Part B: Find the intervals of increase and decrease, and the local and maximum and minimum values.
$$f(x)=(3x-1)/(x-1)^2$$
$$f'(x)=((x-1)^2(3)-(3x-1)(2(x-1)*(1)))/((x-1)^2)^2$$
$$f'(x)=((3(x-1)^2)-(2(3x-1)(x-1)))/(x-1)^3$$
$$f'(x)=(3x-3-6x+2)/(x-1)^3$$
$$f'(x)=(-3x-1)/(x-1)^3$$
So then we can solve for the Critical Points:
We know $$x\ne1 $$and $$-3x-1=0 \implies x=-1/3$$
If we then take $$f(-1/3)=(3x-1)/(x-1)^2$$ we get $$f(-1/3)=-9/8$$
So our intervals are $$(-\infty,-1/3),(-1/3,1),(1,\infty)$$
[table="width: 500, class: grid"]
[tr]
[td][/td]
[td]$$-3x-1$$[/td]
[td]$$x-1$$[/td]
[td]$$f'(x)$$[/td]
[/tr]
[tr]
[td]$$(-\infty,-1/3)$$[/td]
[td]$$+$$[/td]
[td]$$-$$[/td]
[td]decreasing[/td]
[/tr]
[tr]
[td]$$(-1/3,1)$$[/td]
[td]$$-$$[/td]
[td]$$-$$[/td]
[td]increasing[/td]
[/tr]
[tr]
[td]$$(1,\infty)$$[/td]
[td]$$-$$[/td]
[td]$$+$$[/td]
[td]decreasing[/td]
[/tr]
[/table]
Based on the table, we can tell which intervals are increasing and decreasing and that the local minimum is $$f(-1/3)=-9/8$$ and since we have a vertical asymptote at 1, there is no local max.
Part C: Find the intervals of concavity, and the inflection points of $$f$$.
$$f'(x)=(-3x-1)/(x-1)^3$$
$$f''(x)=(((x-1)^3)(-3)-(-3x-1)(3(x-1)^2*(1)))/((x-1)^3)^2$$
$$f''(x)=((-3(x-1)^3)-3(x-1)^2(-3x-1)/(x-1)^6$$
$$f''(x)=(-3(x-1)^2((x-1)+(-3x-1)))/(x-1)^6$$
$$f''(x)=(-3(-2x-2))/(x-1)^4$$
$$f''(x)=(6(x+1))/(x-1)^4$$
So then we can solve for the Critical Points:
We know $$x\ne1 $$and $$x+1=0 \implies x=-1$$
If we then take $$f(-1)=(3x-1)/(x-1)^2$$ we get $$f(-1)=-1$$
So our intervals are $$(-\infty,-1),(-1,1),(1,\infty)$$
[table="width: 500, class: grid"]
[tr]
[td][/td]
[td]$$x+1$$[/td]
[td]$$x-1$$[/td]
[td]$$f''(x)$$[/td]
[/tr]
[tr]
[td]$$(-\infty,-1)$$[/td]
[td]$$-$$[/td]
[td]$$-$$[/td]
[td]concave up[/td]
[/tr]
[tr]
[td]$$(-1,1)$$[/td]
[td]$$+$$[/td]
[td]$$-$$[/td]
[td]concave down[/td]
[/tr]
[tr]
[td]$$(1,\infty)$$[/td]
[td]$$+$$[/td]
[td]$$+$$[/td]
[td]concave up[/td]
[/tr]
[/table]
Based on the table, we can tell the concavity of the intervals and that an inflection point exists at $$f(-1)=-1$$ and since we have a vertical asymptote at 1, there is no inflection at 1.
Part D: Combine all the information from Part A-C and sketch the function.
I am currently working on this part and will post it once I am done.
Will someone let me know if I approaching this correctly?? Thank you.
Last edited: