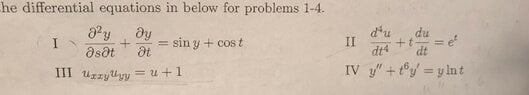Can You Solve These Challenging ODE Exam Questions?

[perlarb]

Hi, I need to do these for an exam and I can't find any way to solve them with what my professor has taught. If you can help me answer even just one of them I'd be very grateful!

1. Which of the differential equations is/are non linear?
a. Only I
b. Only II
c. Only I and III
d. Only II and IV
e. None of the above
View attachment 8462

2. Which is a solution to the following DE? yy'-ye^t=t²e^2t
a. y=t²(e^t)
b. y= (t-1)e^t (Incorrect answer)
c. y= te^t
d. y= (t+1)e^t
e. None of the above

3. For the linear DE xy'=x⁴e^x+2y which of the following is an integrating factor 𝜇(x)?
a. x³
b. x^-3
c. e^x
d. xe^x
e. None of the above (My professor says this is NOT the correct answer).

4. Given that y1= x is a solutio to x²y''+xy'-y=0, x>0, Find the other fundamental solution.
a. y2=x^-2
b. y2=x^-1
c. y2=x
d. y2= x² (Incorrect answer)
e. None of the above

 

[HOI]

For the first one, at least you just need to know the definition of "non-linear". Didn't your teacher mention that? In (I), the dependent function is y and sin(y) is not linear. In (III) the dependent variable is u and $$u_{xxy}u_{yy}$$, the product of two derivatives of u, is non-linear.

For problem 2, differentiate each of the given functions, put the functions and their derivatives into the equation and see if the equation is satisfied._

For problem 3, do you know what an "integrating factor" is? The given equation can be written $$xdy- (x^4e^x+ 2y)dx= 0$$. An "integrating factor is a function f(x,y) such that $$f(x,y)x dy- f(x, y)(x^4e^x+ 2y)dx$$ is an "exact differential"- that is, that there exist F(x,y) such that $$dF= F_xdx+ F_ydy= f(x,y)x dy- f(x, y)(x^4e^x+ 2y)dx$$. One of the conditions for that is that $$(F_{x})_y= (f(x,y)x)_y= (f(x,yx^4e^x+ 2y)_x= (F_y)_x$$. You can use that to derive a differential equation for f(x,y) but here, since you are given possible functions, the simplest thing to do is try each and see which works.

For problem 4, given that y(x)= x is a solution, try a solution of the form y= xu(x). Then y'= u+ xu' and y''= 2u'+ xu''. The differential equation becomes $$x^2y''+ xy'- y= 2x^2u' + x^3u''+ xu+ x^2u'- xu= x^3u''+ 3x^2u'= 0$$. Notice that the "u" terms cancel- that is the result of the fact that x is a solution to the equation. If we let v= u', then the equation becomes $$x^3v'+ 3x^2v= 0$$. That is separable- $$x^3(dv/dx)= -3x^2v$$ so that $$(1/v)dv= (-3/x)dx$$. Integrate both sides- that will give logarithms and then you can take the exponential to get v as a function of x. Integrate v to get u(x) and the other solution is Xu(x).

HOWEVER, again you are given a list of possible solutions. The simplest thing to do is to ignore the "y= x" hint, take the first and second derivatives of each of the given functions and see which actually satisfies the equation!