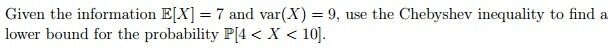Chebyshev Inequality: Get Expert Help Now

  • Context: MHB 
  • Thread starter Thread starter nacho-man
  • Start date Start date
  • Tags Tags
    Inequality
Click For Summary
SUMMARY

The discussion focuses on the application of Chebyshev's Inequality, which states that for a random variable X with mean μ and variance σ², the probability that X deviates from its mean by k or more is bounded by P{|X - μ| ≥ k} ≤ σ²/k². In this specific case, with σ² = 9 and k = 3, the inequality indicates that the probability P is less than or equal to 1, leading to the conclusion that 1 - P is non-negative. This provides a foundational understanding of the inequality's implications in probability theory.

PREREQUISITES
  • Understanding of random variables and their properties
  • Familiarity with statistical concepts such as mean and variance
  • Basic knowledge of probability theory
  • Ability to interpret mathematical inequalities
NEXT STEPS
  • Study the derivation and proof of Chebyshev's Inequality
  • Explore applications of Chebyshev's Inequality in real-world scenarios
  • Learn about other probability inequalities, such as Markov's Inequality
  • Investigate the implications of variance in statistical analysis
USEFUL FOR

Students in statistics, data analysts, and professionals in fields requiring probabilistic modeling will benefit from this discussion, particularly those looking to deepen their understanding of Chebyshev's Inequality and its applications.

nacho-man
Messages
166
Reaction score
0
Could I get some help with this question?
Please refer to the attachment.

Thanks
 

Attachments

  • chebyshev.jpg
    chebyshev.jpg
    6.4 KB · Views: 85
Physics news on Phys.org
nacho said:
Could I get some help with this question?
Please refer to the attachment.

Thanks

The Chebysheff inequality extablishes that for a r.v. X with mean $\mu$ and variance $\sigma^{2}$ for $k \ge 0$ is...

$\displaystyle P \{|X - \mu| \ge k \} \le \frac{\sigma^{2}}{k^{2}}\ (1)$

In Your case is $ \sigma^{2}= 9$ and $k = 3$, so that the (1) supplies $\displaystyle P \le 1 \implies 1 - P \ge 0 $... an 'information' we have independently from Mr Chebysheff (Emo)...

Kind regards

$\chi$ $\sigma$
 

Similar threads

High School Chebyshev inequality, confidence intervals, etc
  • · Replies 6 ·
Replies
6
Views
4K
Undergrad On Jensen's inequality for conditional expectation
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Understanding Jensen's Inequality: Equal Conditions
  • · Replies 5 ·
Replies
5
Views
3K
Graduate Mathematical inequality measures for the social sciences
  • · Replies 12 ·
Replies
12
Views
1K
MHB Prove AM-GM Inequality: What Values to Use?
  • · Replies 3 ·
Replies
3
Views
3K
Undergrad Are There Any Theorems Relating Joint Distributions to Marginals?
  • · Replies 7 ·
Replies
7
Views
3K
High School Bunkbed Conjecture Debunked?
  • · Replies 0 ·
Replies
0
Views
2K
Undergrad Bohmian Prediction of Bell Inequality Violations
  • · Replies 45 ·
2
Replies
45
Views
5K
MHB Properties of the Ordinals ....
  • · Replies 1 ·
Replies
1
Views
1K
MHB What Are the Solutions to the System of Inequalities for Target Heart Rate?
  • · Replies 3 ·
Replies
3
Views
1K