- #1
Master1022
- 590
- 116
- Homework Statement
- How many quadrilaterals are there?
- Relevant Equations
- Combinatorics
Hi,
I was watching a Youtube on combinatorics (here) and a problem was posed at the end of the video about counting the number of quadrilaterals.
Question:
How many quadrilaterals are present in the following pattern?
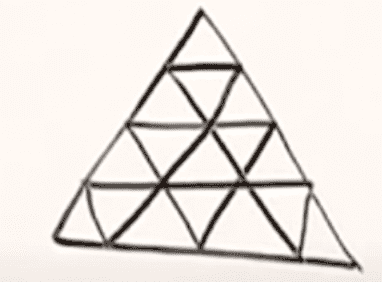
Attempt:
The video started with the simpler problem of finding the number of quadrilaterals in the following shape (a single 'strip' of the triangle):
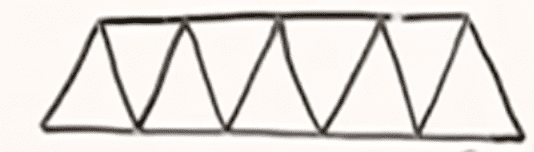
The way I thought about it was that the quadrilateral was formed by taking two horizontal lines and two diagonal lines:
\begin{pmatrix} 2 \\ 2 \end{pmatrix} \cdot \begin{pmatrix} 10 \\ 2 \end{pmatrix}
However, the individual triangles need to be deducted from the above product: there are ## = 2(5) - 1 = 9 ## individual triangles. Thus, I have:
\begin{pmatrix} 2 \\ 2 \end{pmatrix} \cdot \begin{pmatrix} 10 \\ 2 \end{pmatrix} - 9 = 45 - 9 = 36 quadrilaterals
Now that I completed that basic problem, I am thinking how to extend that concept to the larger triangle case. I am trying to avoid a laborious method of looking at each row doing lots of sums because I hope that there is an elegant solution.
Currently, all I can think of is doing is:
\begin{pmatrix} \text{number of small triangles} \\ 2 \end{pmatrix} = \begin{pmatrix} 25 \\ 2 \end{pmatrix}.
This is because we can pick two triangles and form a quadrilateral between them.
Does this seem like it is headed along the correct path?
Any help is greatly appreciated.
I was watching a Youtube on combinatorics (here) and a problem was posed at the end of the video about counting the number of quadrilaterals.
Question:
How many quadrilaterals are present in the following pattern?
Attempt:
The video started with the simpler problem of finding the number of quadrilaterals in the following shape (a single 'strip' of the triangle):
The way I thought about it was that the quadrilateral was formed by taking two horizontal lines and two diagonal lines:
\begin{pmatrix} 2 \\ 2 \end{pmatrix} \cdot \begin{pmatrix} 10 \\ 2 \end{pmatrix}
However, the individual triangles need to be deducted from the above product: there are ## = 2(5) - 1 = 9 ## individual triangles. Thus, I have:
\begin{pmatrix} 2 \\ 2 \end{pmatrix} \cdot \begin{pmatrix} 10 \\ 2 \end{pmatrix} - 9 = 45 - 9 = 36 quadrilaterals
Now that I completed that basic problem, I am thinking how to extend that concept to the larger triangle case. I am trying to avoid a laborious method of looking at each row doing lots of sums because I hope that there is an elegant solution.
Currently, all I can think of is doing is:
\begin{pmatrix} \text{number of small triangles} \\ 2 \end{pmatrix} = \begin{pmatrix} 25 \\ 2 \end{pmatrix}.
This is because we can pick two triangles and form a quadrilateral between them.
Does this seem like it is headed along the correct path?
Any help is greatly appreciated.