Condition for a vector field be non-linear

[Jhenrique]

If a vector field $\vec{v}$ is non-divergent, so the identity is satisfied: $\vec{\nabla}\cdot\vec{v}=0$;

if is non-rotational: $\vec{\nabla}\times\vec{v}=\vec{0}$;

but if is "non-linear"

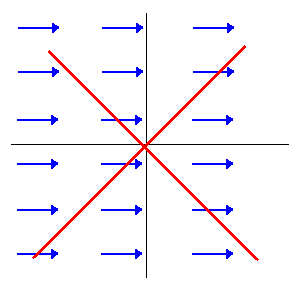
Which differential equation the vector $\vec{v}$ satisfies?

EDIT: this isn't an arbritrary question, is an important question, because the Helmholtz-Hodge decomposition says that every vector field can be decompost in a divergent vector field + a rotational vector field + a linear vector field.

 

[Greg Bernhardt]

I'm sorry you are not generating any responses at the moment. Is there any additional information you can share with us? Any new findings?

 

[Matterwave]

I have never seen a source that says you have to add a "linear vector field".

http://en.wikipedia.org/wiki/Helmholtz_decomposition

This article seems to not require such a "linear vector field". You have to give some context to the question. Perhaps a source with your statement.

 

[Terandol]

This question in fact brings up an interesting point about the uniqueness of the Helmholtz theorem which is often omitted. In Helmholtz's original paper on fluid dynamics he does in fact include a third term in the decomposition which he calls a "translation" term. Essentially, what you refer to as the "linear" term in the decomposition results from the fact that unless some boundary conditions or decay conditions are specified, the Helmholtz decomposition is not unique.

The Hodge decomposition theorem says
<br /> <br /> E^p(M)=d(E^{p-1})\oplus \delta(E^{p+1}) \oplus H^p<br /> <br />

where E^p(M) is the space of smooth p-forms on the manifold M, d is the differential, \delta=(\pm 1) * d * is the codifferential and H^p is the space of all harmonic p-forms (ie. 0=\Delta\omega=(d\delta+\delta d)\omega. ) Then what you are calling a linear vector field is given by the equation \Delta \omega =0. It is straightforward to show, using the fact that \delta is the adjoint of d, that \Delta\omega=0 if and only if d\omega=0 and \delta \omega =0.

In your specific case, you can phrase this theorem in terms of vector fields (ie. turn the Hodge decomposition into the Helmholtz decomposition) by using the usual identification of vector fields with both one forms and two forms in \mathbb{R}^3 (note that we must restrict to bounded domains or forms that decay quickly enough since this is not a compact manifold.) Then d on one forms becomes the curl, \delta on one forms becomes the divergence, d on 0-forms becomes the gradient and \delta on 2-forms is the curl. So the Hodge decomposition becomes exactly the Helmholtz decomposition just with an extra harmonic term added.

Further the harmonic condition \Delta \omega=0 translates into the two conditions \mathrm{div}(\vec V)=0 and \mathrm{curl}(\vec{V})=0 under our identifications. These two conditions define what you mean when you say a "linear" vector field (at least they make the decomposition theorem work.) Note that it is also possible to write this harmonic term as the gradient of a scalar potential or the curl of a vector potential, so the harmonic term kind of gathers together the non-uniqueness of the potentials in the decomposition into a single term.

If you are in infinite space then the decay condition forces the vector field to go to zero at infinity, and this forces the harmonic term to vanish also. However, if you are in a bounded domain, then you can get a nonzero harmonic term and so the Helmholtz decomposition is not unique and boundary conditions are required to uniquely specify a decomposition.

If you want the tl;dr version, the Helmholtz theorem says any vector field on a compact manifold (or a vector field which decays sufficiently rapidly on a noncompact manifold) can be uniquely decomposed as
\vec W=\nabla\Phi+\mathrm{curl}(\vec A)+\vec Z
where \Phi is a scalar potential (ie. a smooth function), \vec A is a vector potential (ie. a vector field or equivalently a two-form) and \vec Z is harmonic (ie. a harmonic one-form which corresponds to a vector field satisfying \mathrm{curl}(\vec Z)=0=\mathrm{div}(\vec Z).) However, when decay conditions are specified, the harmonic term is zero and so this term is omitted when it is understood that the vector field decays at infinity.