njvc3
- 4
- 0
Hello, I was looking for some help. please...
I've been struggling with the following problem:
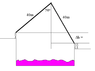
Jane, whose mass is 50kg, needs to swing across a river filled with crocs in order rescue Tarzan, whose mass is 80kg. However, she must swing into a constant horizontal wind Force (110 N) on a vine (L=40m) that is initially at an angle of (theta=50) with the vertical. and the distance of the river she must cross is D=50 m. (The diagram displays the height Jane is at inititally to be a little higher than the height of the bank Tarzan is at)
a) What is the minimum speed Jane must begin her swing in order to just make it to the other side?
b) Once the rescue is complete, Tarzan and Jane must swing back together across the river. What is the minimum speed they must begin their swing?
I tried to figure out the height by figuring out how much Potential Energy she has.. Change in net Energy is 0; so using the Conservation of Energy equation: delta KE + delta Epot + deltaEwind = 0
figuring the final velocity (that she lands at) is 0 and the change in final height is 0... I'm left with the following equation:
(1/2m*(initial v)^2)+(m*g*delta h initial)-(Force wind*D)
where the only information I don't have is the initial v and delta h initial.
The answers are supposed to be a)6.15m/s & b) 9.87m/s ... but, i can't seem to get it..
Thanks.
I've been struggling with the following problem:
Jane, whose mass is 50kg, needs to swing across a river filled with crocs in order rescue Tarzan, whose mass is 80kg. However, she must swing into a constant horizontal wind Force (110 N) on a vine (L=40m) that is initially at an angle of (theta=50) with the vertical. and the distance of the river she must cross is D=50 m. (The diagram displays the height Jane is at inititally to be a little higher than the height of the bank Tarzan is at)
a) What is the minimum speed Jane must begin her swing in order to just make it to the other side?
b) Once the rescue is complete, Tarzan and Jane must swing back together across the river. What is the minimum speed they must begin their swing?
I tried to figure out the height by figuring out how much Potential Energy she has.. Change in net Energy is 0; so using the Conservation of Energy equation: delta KE + delta Epot + deltaEwind = 0
figuring the final velocity (that she lands at) is 0 and the change in final height is 0... I'm left with the following equation:
(1/2m*(initial v)^2)+(m*g*delta h initial)-(Force wind*D)
where the only information I don't have is the initial v and delta h initial.
The answers are supposed to be a)6.15m/s & b) 9.87m/s ... but, i can't seem to get it..
Thanks.