Marbig
- 3
- 0
Hi all,
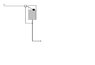
I got the system (attached below) and I am trying to work out the following (at point x-outflow):
-net head of the system (I guess this isn't really at point x)
-flow rate
-pressure
I know the flowrate and pressure at point Y, I also know how high the water in the tank is at equilibrium (relative to point x) and I also know the frictional losses in the pipe. Now the ball on the tank is an equilibrium valve.
I have been told that the tank is a constant head tank, I know that means that it will maintain a constant head during the operation.
So I am a bit stuck on working out flow rate, pressure and net head at point x.
Here is what I think:
The net head of the system is basically the height between the water in the tank and point x
To work out the flow at point-X. I can apply bernoulli's equation between points y and x. I know Py, Vy,Hy...however all I know at x is Hx.
Thank you in advance for any assistance.
I got the system (attached below) and I am trying to work out the following (at point x-outflow):
-net head of the system (I guess this isn't really at point x)
-flow rate
-pressure
I know the flowrate and pressure at point Y, I also know how high the water in the tank is at equilibrium (relative to point x) and I also know the frictional losses in the pipe. Now the ball on the tank is an equilibrium valve.
I have been told that the tank is a constant head tank, I know that means that it will maintain a constant head during the operation.
So I am a bit stuck on working out flow rate, pressure and net head at point x.
Here is what I think:
The net head of the system is basically the height between the water in the tank and point x
To work out the flow at point-X. I can apply bernoulli's equation between points y and x. I know Py, Vy,Hy...however all I know at x is Hx.
Thank you in advance for any assistance.