MHB Convex Quadrilateral Problem: Prove Inequality with Diagonal Point T

[MarkFL]

Here is this week's POTW:

---

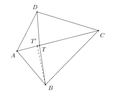
Let $ABCD$ be a convex quadrilateral with $\overline{AB}=\overline{AD}$. Let $T$ be a point on the diagonal $\overline{AC}$ such that $\angle ABT+\angle ADT=\angle BCD$.

Prove that $\overline{AT}+\overline{AC}\ge\overline{AB}+\overline{AD}$.

---

anemone will be grading this week's problem, and will be back to posting the problems next week. (Smile)

Remember to read the http://www.mathhelpboards.com/showthread.php?772-Problem-of-the-Week-%28POTW%29-Procedure-and-Guidelines to find out how to http://www.mathhelpboards.com/forms.php?do=form&fid=2!

 

[anemone]

I would like to give a vote of thanks to MarkFL for standing in for me while I was unavailable to handle my POTW duties. (Handshake) (Smile)

No one answered last week's problem. You can find the suggested solution below:

Spoiler

View attachment 7881
On the segment $\overline{AC}$, consider the unique point $T'$ such that $\overline{AT}'\cdot\overline{AC}=\overline{AB}^2$. The triangles $ABC$ and $AT'B$ are similar: they have the angle at $A$ common and $\overline{AT}':\overline{AB}=\overline{AB}:\overline{AC}$. So $\angle ABT'=\angle ACB$. Analogously, $\angle ADT'=\angle ACD$. So $\angle ABT'+\angle ADT'=\angle BCD$. But $ABT'+ADT'$ increases strictly monotonously, as $T'$ moves from $A$ towards $C$ on $\overline{AC}$. The assumption on $T$ implies that $T'=T$. So, by the arithmetic-geometric mean inequality,$$\overline{AB}+\overline{AD}=2\overline{AB}=2\sqrt{\overline{AT}\cdot\overline{AC}}\le\overline{AT}+\overline{AC}$$