Could use some help for this statistics/math problem

  • MHB
  • Thread starter kimchuu
  • Start date
In summary, the speaker is seeking help with two questions that are due tomorrow. They are unsure about the answers and are asking for clarification. They also mention another problem they are having with a graph that they believe is drawn incorrectly. They are uncertain about the shape of the graph and are seeking assistance.
  • #1
kimchuu
3
0
Hello Everyone!
I really need help on 2 questions and it is due tomorrow! So please help me when u can and ASAP

1653533132259.png

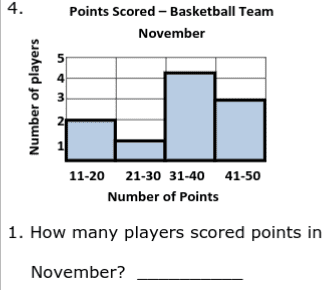
So for this one, this was easy, except for the 31-40 interval I'm not sure if it's 4.5, cause it's not necessarily exactly between and half of 4 and 5 and for the 41-50 interval I'm not sure if its actually a 3 and its somewhat confusing. Does anyone care to enlighten me?
1653533246775.png

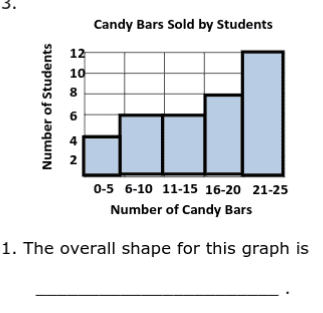
For this one, I am also confused. For my answer I believe it is approximately symmetric, you know what I did? So I did like what you usually do I add and replace the bars so all of them can look symmetric,
and then for the last one it stays as 12 and if I break/divide it by 2, you get 6, and that will be perfectly symmetric. The thing is I don't know if my thesis is correct.
PLEASE KINDLY
HELP ME ASAP
 
Mathematics news on Phys.org
  • #2
I would say that the first one is just drawn badly! They did NOT have a fractional number of players on the floor! There were 2+ 1+ 4+ 3= 10 players.

For the next one, I have no idea what they mean by "shape"! I would probably say that this graph is shaped like a staircase!
 
  • Like
Likes roam

FAQ: Could use some help for this statistics/math problem

What is the problem asking for?

The problem is asking for assistance in solving a statistics or math problem. It could involve calculating a specific value, interpreting data, or understanding a concept.

Can you provide any background information on the problem?

Yes, it is important to provide any relevant information such as the given data or variables, the context of the problem, and any known equations or formulas that may be applicable.

How should I approach solving the problem?

First, carefully read and understand the problem. Then, identify any relevant equations or formulas and apply them to the given information. If necessary, break down the problem into smaller, more manageable steps. Finally, check your work and make sure the solution makes sense in the context of the problem.

What if I am still stuck on the problem?

If you are still struggling to solve the problem, it may be helpful to seek out additional resources such as textbooks, online tutorials, or asking a classmate or teacher for assistance. It is important to not get discouraged and to keep practicing and learning.

How can I improve my skills in solving statistics/math problems?

The best way to improve your skills is to practice regularly and seek out additional resources such as textbooks, online tutorials, or workshops. It is also helpful to review and understand any mistakes you may have made in the past and to continuously challenge yourself with new and more complex problems.

Similar threads

MHB Could use some help for this statistics/math problem
Replies
2
Views
934
MHB Needed some help with this organizational problem
Replies
2
Views
1K
I Derivation of equations using tensor
Replies
1
Views
1K
I Subgroup axioms for a symmetric group
Replies
1
Views
943
MHB Fourier Series involving Hyperbolic Functions
Replies
9
Views
3K
MHB Are These Statistics Practice Answers Correct?
Replies
1
Views
2K
I Problems involving combinatorics of lattice with certain symmetries
Replies
2
Views
984
I Video on imaginary numbers and some queries
Replies
2
Views
1K
MHB Evaluate Inverse of Hi M.H.B.: Math Problem
Replies
3
Views
3K
MHB Why I Get X & Y Mixed Up When Plotting Graphs
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top