Count and Categorical Variables...

[fog37]

TL;DR

Count and Categorical Variables...

Hello,
In the context of categorical variables, a frequency table which gives us the count (aka frequency) for each level of the categorical variable. Count is a number telling us how many times a specific level occurs. A bar-chart handles a single categorical variable (nominal or ordinal) with its levels indicated on the x-axis and count (frequency), or relative frequency, on the y-axis.

My question: is count a discrete non-negative numerical variable? If not, what is it? I don't think it is a numerical variable...
Can count ever be represented as one of the axes of a scatterplot? A scatterplot is designed to accommodate two numerical variables (both discrete, both continuous, one discrete and one continuous) on its two axes.

Here another example that confuses me: a dataset where each row represents a different country and there is a variable that reports the percentage of the country population who is religious (which is the count of people who responded YES to being religious divided by the total country population). That column contains % values and seems to represent a numeric variable even if it represents the relative count of a categorical variable. Is that correct? See attached table:

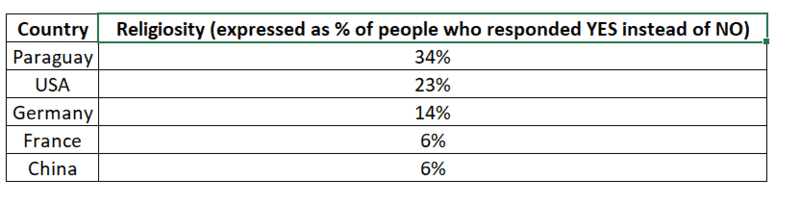
Also, cost and profit are generally considered continuous variables but I believe they are discrete numeric variables since money is a multiple of the cent, the smallest increment. When we build a histogram, we bin the continuous variable values into intervals. Does that turn the continuous variable into an ordinal categorical variable since the data now belongs in a finite number of groups?

Thank you!

 

[Dale]

My question: is count a discrete non-negative numerical variable?

It certainly could be.

If not, what is it?

It is a summary statistic.

Can count ever be represented as one of the axes of a scatterplot?

Sure. Just like you could put medians or standard deviations on one of the axes of a scatter plot you could also put counts on an axis of a scatter plot.

Does that turn the continuous variable into an ordinal categorical variable since the data now belongs in a finite number of groups?

It could if you wanted to.

 

[FactChecker]

My question: is count a discrete non-negative numerical variable? If not, what is it? I don't think it is a numerical variable...

It is a natural number (where 0 is included). They are ordered and have arithmetic properties.

Can count ever be represented as one of the axes of a scatterplot? A scatterplot is designed to accommodate two numerical variables (both discrete, both continuous, one discrete and one continuous) on its two axes.

I wouldn't call it a "scatter plot", but you certainly can make charts where the categories are along one axis, in order of the count. It happens all the time when you are interested in what category occurs the most. From https://inferentialthinking.com/chapters/07/1/Visualizing_Categorical_Distributions.html:

Here another example that confuses me: a dataset where each row represents a different country and there is a variable that reports the percentage of the country population who is religious (which is the count of people who responded YES to being religious divided by the total country population). That column contains % values and seems to represent a numeric variable even if it represents the relative count of a categorical variable. Is that correct? See attached table:

View attachment 322281

Also, cost and profit are generally considered continuous variables but I believe they are discrete numeric variables since money is a multiple of the cent, the smallest increment. When we build a histogram, we bin the continuous variable values into intervals. Does that turn the continuous variable into an ordinal categorical variable since the data now belongs in a finite number of groups?

No. The counting numbers have too many arithmetic properties to just be considered "categorical". They are ordered. You can add them. You can subtract them, although it might give a negative result. You can divide them if you allow rational numbers. The natural numbers are a subset of the integers, the rational numbers, and the real numbers and should not be considered only "categorical".

 

[andrewkirk]

When we build a histogram, we bin the continuous variable values into intervals. Does that turn the continuous variable into an ordinal categorical variable since the data now belongs in a finite number of groups?

It doesn't "turn it into" a categorical variable, but it creates a new categorical variable. If the original continuous variable was 'income' we could call the new categorical variable 'income range'.
I occasionally work on health system patient data which, amongst hundreds of variables, has age (of patient at time of recorded health system interaction) - a floating point variable, and 'age-range' a categorical variable that classifies patients into 5-year age ranges. Although the database provides both variable, we could just read in 'age' and derive 'age range' from 'age'.