mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
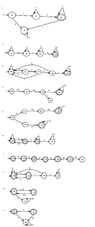
I have to draw the DFA's for the following languages:
$\Sigma=\{0, 1\}$
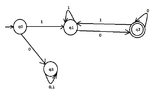
View attachment 4142
Could you tell me if it is correct?? (Wondering)
Could you give me some hints how we could find the DFA of the last three languages ?? (Wondering)
I have to draw the DFA's for the following languages:
$\Sigma=\{0, 1\}$
- $$\{w \mid w \text{ starts with } 1 \text{ and ends with } 0 \}$$
- $$\{w \mid w \text{ contains at least 3 } 1\}$$
- $$\{w \mid w \text{ contains the substring } 0101\}$$
- $$\{w \mid w \text{ has length at least } 3 \text{ and the third symbol is } 0\}$$
- $$\{w \mid w \text{ starts with } 0 \text{ and has an odd length, or with } 1 \text{ and has an even length} \}$$
- $$\{w \mid w \text{ doesn't contain the substring } 110\}$$
- $$\{w \mid \text{ the length of } w \text{ is smaller than or equal to } 5\}$$
- $$\{w \mid w \text{ is any string besides } 11 \text{ and } 111\}$$
- $$\{w \mid \text{ in each odd position of } w \text{ there is a } 1\}$$
- $$\{w \mid w \text{ contains at least two } 0 \text{ and at most one } 1\}$$
- $$\{\epsilon , 0\}$$
- $$\{w \mid w \text{ contains an even number of } 0, \text{ or exactly two } 1\}$$
- the empty set
- all strings besides the empty one.
View attachment 4142
Could you tell me if it is correct?? (Wondering)
Could you give me some hints how we could find the DFA of the last three languages ?? (Wondering)
Attachments
Last edited by a moderator: