Discussion Overview
The discussion revolves around the concept of infinity and the enumeration of rational numbers, particularly in relation to Cantor's work. Participants explore the implications of Cantor's diagonal argument and the nature of bijections between sets, focusing on whether all rational numbers can be listed or enumerated in correspondence with natural numbers.
Discussion Character
- Debate/contested
- Mathematical reasoning
Main Points Raised
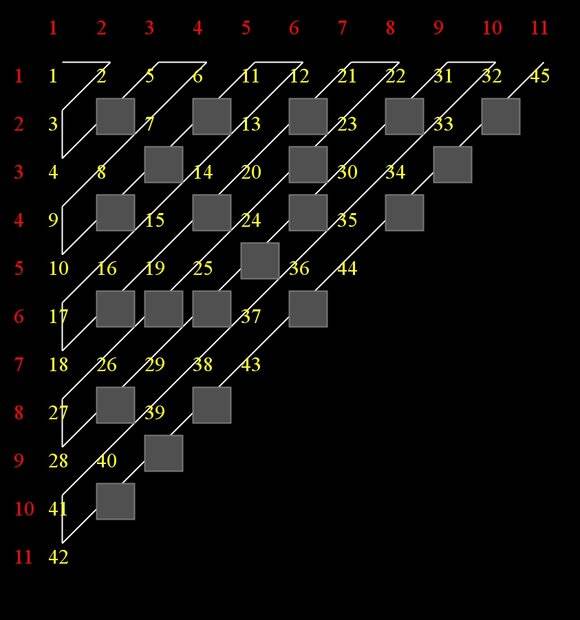
- Some participants assert that Cantor demonstrated that not all real numbers can be enumerated, while rational numbers can be, using a grid to illustrate this point.
- Others challenge the validity of the proposed grid, arguing that it does not correctly establish a bijection between rational numbers and natural numbers due to potential duplicates in the listing.
- One participant questions the necessity of a "goal" for a bijection, suggesting that skipping duplicates could still yield a valid correspondence.
- Another participant raises a concern about the ability to determine specific rational numbers corresponding to large natural numbers without an algorithm, implying that such a bijection may not be practically useful.
- Some participants argue that the existence of a bijection does not require it to be easily computable or straightforward to follow.
Areas of Agreement / Disagreement
Participants express disagreement regarding the validity of the proposed enumeration of rational numbers and the implications of Cantor's work. There is no consensus on the correctness of the arguments presented, and multiple competing views remain.
Contextual Notes
Participants reference the concept of bijections and the nature of enumeration, but there are unresolved issues regarding the treatment of duplicates and the practical implications of the proposed mappings.