De1.2.1 Solve the following initial value problem

[karush]

$\tiny{de1.2.1}$
$\textsf{ Solve each of the following initial value problems and plot the solutions for several values of $y_0$.}\\$
$\textsf{ Then describe in a few words how the solutions resemble, and differ from, each other.}\\$
$$\begin{align*}\displaystyle
\frac{dy}{dt}&=-y+5, \quad y(0)=y_0\\
y'&=-y+5\\
y'+y&=5\\
u(t)&=\exp\int \, dt = e^t\\
e^ty'+e^ty&=e^t5\\
(e^ty)'&=e^t5\\
e^ty &=5\int e^t dt=5e^t+c\\
y &=5+\frac{c}{e^t}\\
y(0)&=5+c
\end{align*}$$
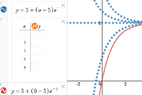
$\textit{ok not sure where I went off the rails but the book answer is}\\$ $$y=5+(y_0-5)e^{-t}$$
$\textit{also not sure how this would be set up in Desmos}$

 

[MarkFL]

You correctly stated:

$$y(0)=5+c$$

You just need to add:

$$y(0)=5+c=y_0\implies c=y_0-5$$

And so your solution is:

$$y(y)=5+\left(y_0-5\right)e^{-t}$$

I would use a Desmos slider:

[DESMOS]advanced: {"version":5,"graph":{"squareAxes":false,"viewport":{"xmin":-10,"ymin":-10,"xmax":10,"ymax":10}},"expressions":{"list":[{"type":"expression","id":"graph1","color":"#2d70b3","latex":"y=5+\\left(a-5\\right)e^{-x}","style":"SOLID"},{"type":"expression","id":"2","color":"#388c46","latex":"a=0","hidden":true,"style":"SOLID"}]}}[/DESMOS]

Now, manually move or animate the slider to see how the solution behaves for differing values of the parameter.

 

[karush]

thank you
I got ? on $y_0$ thing

so multiple graphs would just be $y(1) \quad y(2) \cdots$ for $y(a)$ ?

 

[MarkFL]

thank you
I got ? on $y_0$ thing

so multiple graphs would just be $y(1) \quad y(2) \cdots$ for $y(a)$ ?

I'm not sure I know what you mean. If you want multiple graphs, you could just define them like this:

[DESMOS]advanced: {"version":5,"graph":{"squareAxes":false,"viewport":{"xmin":-10,"ymin":-10,"xmax":10,"ymax":10}},"expressions":{"list":[{"type":"expression","id":"graph1","color":"#2d70b3","latex":"y=5+\\left(-10-5\\right)e^{-x}","style":"SOLID"},{"type":"expression","id":"2","color":"#388c46","latex":"y=5+\\left(-5-5\\right)e^{-x}","style":"SOLID"},{"type":"expression","id":"3","color":"#fa7e19","latex":"y=5+\\left(0-5\\right)e^{-x}","style":"SOLID"},{"type":"expression","id":"4","color":"#6042a6","latex":"y=5+\\left(5-5\\right)e^{-x}","style":"SOLID"},{"type":"expression","id":"5","color":"#000000","latex":"y=5+\\left(10-5\\right)e^{-x}","style":"SOLID"},{"type":"expression","id":"6","color":"#c74440","latex":"y=5+\\left(15-5\\right)e^{-x}","style":"SOLID"}]}}[/DESMOS]

 

[karush]

View attachment 8291

ok I used a table
but ? about where t is

 

[MarkFL]

[DESMOS]advanced: {"version":5,"graph":{"xAxisLabel":"t","yAxisLabel":"y","squareAxes":false,"viewport":{"xmin":-10.72837090838311,"ymin":-10.471822929382325,"xmax":10.52162909161689,"ymax":10.778177070617675}},"expressions":{"list":[{"type":"expression","id":"graph1","color":"#2d70b3","latex":"y=5+\\left(0-5\\right)e^{-t}","style":"SOLID"},{"type":"expression","id":"2","color":"#388c46","latex":"y=5+\\left(10-5\\right)e^{-t}","style":"SOLID"},{"type":"expression","id":"3","color":"#fa7e19","latex":"y=5","style":"SOLID"},{"type":"expression","id":"4","color":"#6042a6","latex":"y=5+\\left(-5-5\\right)e^{-t}","style":"SOLID"},{"type":"expression","id":"5","color":"#000000","latex":"y=5+\\left(15-5\\right)e^{-t}","style":"SOLID"}]}}[/DESMOS]

You can use \(t\) as the independent variable, and even label the axis, as you see above.

 

[karush]

Ok.

But is there negative time
Or past time

 

[MarkFL]

Ok.

But is there negative time
Or past time

Sure, we can consider time before time \(t=0\), depending on what we're modeling. We can say that time \(t=0\) corresponds to out initial observation of the system, where negative values of \(t\) correspond to times before our observation and positive values of \(t\) correspond to times after the initial observation.