Derivation of recovery channel for bit flip error

[steve1763]

TL;DR

I have found a derivation of the recovery channel for a bit flip error (using the derivation of the Knill-Laflamme condition), but dont quite understand it.

In general, if R is the recovery channel of an error channel ε, with state ρ, then

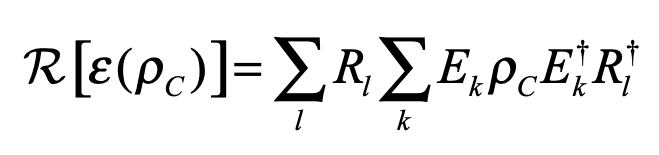
and according to these lecture slides, we get the final result highlighted in red for a bit flip error channel. I am simply asking how one reaches this final result. Thank you (a full-ish derivation can be found at https://orion.math.iastate.edu/ytpoon/publication/qecc1.pdf on pages 6-7, but for some reason i still don't understand how one gets to the final answer).

 

[azntoon]

To get the final result, we start by applying the definition of recovery channel:\begin{align}R(\rho) &= \sum_i A_i \rho A_i^\dagger \\&= \sum_i A_i \rho A_i^\dagger \sum_j B_j \rho B_j^\dagger \\&= \sum_{i,j} A_i \rho A_i^\dagger B_j \rho B_j^\dagger\end{align}Now, for a bit flip error channel, we have $A_i = \sigma_x^i$ and $B_j = \sigma_x^j$. Substituting these values into the equation above gives us\begin{align}R(\rho) &= \sum_{i,j} \sigma_x^i \rho \sigma_x^{i\dagger} \sigma_x^j \rho \sigma_x^{j\dagger} \\&= \sum_{i,j} \sigma_x^i \rho \sigma_x^i \sigma_x^j \rho \sigma_x^j \\&= \sum_{i,j} \sigma_x^{i+j} \rho \sigma_x^{i+j} \\&= \sum_k \sigma_x^k \rho \sigma_x^k\end{align}where $k = i + j$. This is the final result.