Derive 6 Help with Laplace Transforms

[BIGEYE]

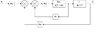
I am new to Derive 6 and Laplace Transforms. Is it possible to solve the closed loop gain A/B of the attached loop using Derive 6. If it is possible, can someone guide me through the steps using Derive, as the problems that lie ahead will be much more complex, and I want to use Derive in the future.

TIA

 

[uart]

Not sure I'm fully understanding what you're asking, but assuming you underdstand how to find the closed loop transfer function in general then it's just a matter of substitution.

That is, H_cl = F/(1+F R)

Where F = Ka Km / (s (1+ sT)) and R = Ki in the example you post.

 

[BIGEYE]

Let me try again!

I made a complete balls of that question, everything was wrong. Let me try again, I have to evaluate the closed loop gain of the loop C/R, using the laplace operator s.
The correct circuit is attached.
I can do this problem manually, but it is very tedious and easy to amke a mistake. I want to know how this can be done using Derive 6, if someone can show me the steps.

TIA

 

[uart]

Well I can't yet see that attachment becasue it's still pending approval but I hope you understand the basic concept here. All you need is simple alegraic substitution, that's it!

It's trivial to show that the closed loop transfer function is F(s)/(1+ F(s)*R(s)). Where F(s) is the transfer function of forward block and R(s) is the transfer function of the feedback block (and * is just normal multiplication). So just subst in the appropriate expressions for F and R, it couldn't be much simpler.