Destructive interference of sound

[sparkle123]

Two loudspeakers are separated by 0.50 m on one wall of a room measuring 3.5 m by 7.0 m at a temperature of 22°C. Both speakers generate a constant amplitude sound of frequency 690 Hz, in phase with each other, radiating equally in all directions. What is the shortest distance x along the adjacent wall where an observer will hear no sound? Ignore any reflections from the walls.

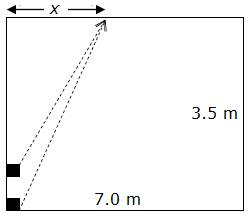
I think that constructive interference means the lengths differ by an odd multiple of half the wavelength (0.249 m).
so sqrt(x^2 + 3.5^2) - sqrt(x^2 + 3^2) = 0.249 (2k + 1)

But this is really complicated...Please give me a hint on how to start?

 

[ehild]

Life is easier if you replace x²+9 by a new variable, say y. Move √y to the right-hand side and square the equation, y will cancel. Solve for √y. Decide what k gives the smallest possible value for it, then compute x.

ehild

 

[sparkle123]

Thanks, but I get a nonreal answer for x. the min of y is 1.064E-12