Discussion Overview
The discussion revolves around determining a suitable contour for the integral
$\displaystyle \int_0^{\infty} \dfrac{\log (x) }{x^2 +1 } dx$. Participants explore various methods and contours in the complex plane, addressing both theoretical and practical aspects of the integration process.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
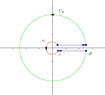
- Some participants propose a contour that includes a semicircle and rays emanating from points on the imaginary axis, suggesting a specific path for integration.
- One participant mentions that a substitution $x \mapsto 1/x$ could simplify the integral, leading to the conclusion that the integral evaluates to zero.
- Another participant argues that the proposed contour might not work due to the behavior of the logarithmic term, suggesting alternative functions or adjustments to the branch cut.
- A later reply discusses integrating a modified function $\frac{\log^2(z)}{z^2+1}$ along a contour, providing a detailed calculation that relates back to the original integral.
Areas of Agreement / Disagreement
Participants express differing views on the suitability of various contours and methods for evaluating the integral. No consensus is reached regarding the best approach or the validity of the proposed contours.
Contextual Notes
Some participants note that previous demonstrations indicate the integral evaluates to zero, while others highlight the challenges in finding a suitable contour in the complex plane. The discussion includes unresolved mathematical steps and assumptions about the behavior of the logarithmic function.