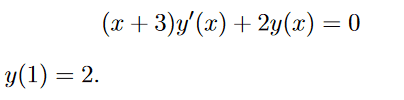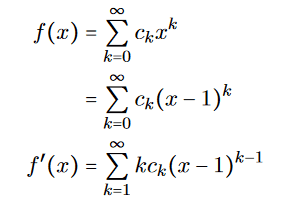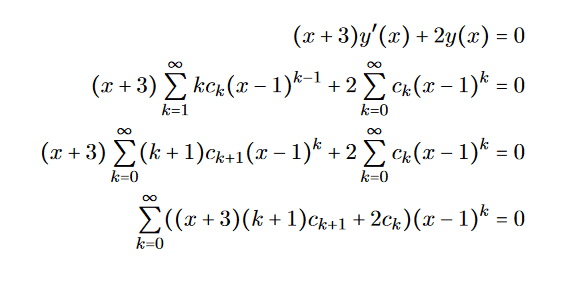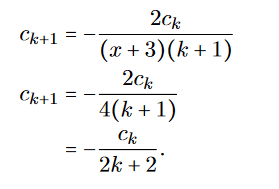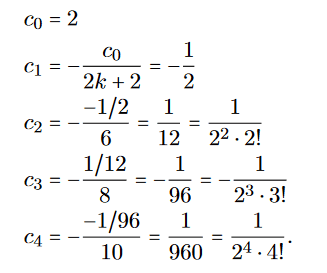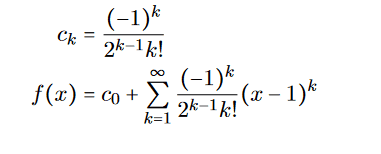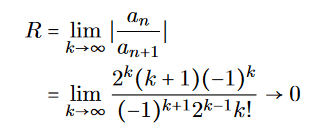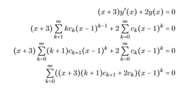Discussion Overview
The discussion revolves around solving a differential equation using the power series method. Participants explore the formulation of the series, the recurrence relations for coefficients, and the implications of boundary conditions.
Discussion Character
- Exploratory
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant expresses doubt about their solution, noting that the convergence radius approaches zero, which seems incorrect given the initial condition y(1)=2.
- Another participant suggests that the coefficients c_k should be independent of x and provides a method to write the derivative in terms of a power series.
- A participant acknowledges trying the suggested method but struggles to derive a general solution, questioning where they might have gone wrong.
- Several participants derive a recurrence relation for the coefficients c_k, indicating it can be solved easily, and mention a general solution form they believe is correct.
- There is a discussion about the manipulation of sums and terms in the power series, with participants clarifying the treatment of the k=0 term in the series.
- One participant points out a fundamental issue regarding the equality of different series representations, emphasizing the importance of correctly handling the terms in the power series.
Areas of Agreement / Disagreement
Participants generally do not reach a consensus, as there are multiple competing views on the correct formulation and manipulation of the power series and the recurrence relations.
Contextual Notes
Some participants express uncertainty about the correctness of their manipulations and the implications of their results, particularly concerning the boundary conditions and convergence of the series.