DLVO Theory of Colloid Stability

[Dario56]

DLVO theory gives the curve of potential energy vs distance of two colloid particles. Potential energy curve is derived for colloids being only electrostatically stabilized and not sterically.

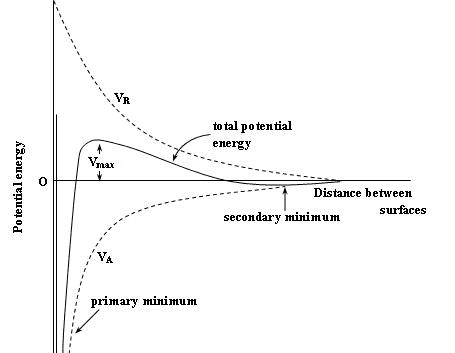
Looking at the image below which shows potential energy curve, we can see two local minima and one maximum. Between local maximum and secondary minimum is a domain of repulsive forces since potential energy increases by making distance between particles smaller.

Theory predicts that if colloid particles have enough energy (usually energy of Brownian motion), they can overcome repulsive forces and bond at primary local minimum which causes flocculation and colloid instability.

If they don't have enough energy colloid should be stable according to this theory, however this doesn't make sense since particles can still bond at secondary minimum. Bonding at secondary minimum forms much weaker bond which can be seen on the curve, but it should still cause particle bonding and flocculation since particles arrive at local minimum.

If this is so, how can this theory predict colloid stability?

 

[TeethWhitener]

In standard DLVO theory, colloids are not thermodynamically stable. The primary minimum is the global energy minimum and represents an aggregated state. And in fact, most colloids will separate if left alone for very long periods of time. However, what DLVO predicts is that colloids can be metastable. That is, $V_{max}$ is essentially the kinetic activation barrier to aggregation, and if it is high enough, then particles separated at infinity will not, on average, have enough energy to overcome the activation barrier and aggregate. In fact, you can use $V_{max}-V(\infty)$ as the activation barrier to estimate the rate at which a colloid aggregates.

 

[Dario56]

In standard DLVO theory, colloids are not thermodynamically stable. The primary minimum is the global energy minimum and represents an aggregated state. And in fact, most colloids will separate if left alone for very long periods of time. However, what DLVO predicts is that colloids can be metastable. That is, $V_{max}$ is essentially the kinetic activation barrier to aggregation, and if it is high enough, then particles separated at infinity will not, on average, have enough energy to overcome the activation barrier and aggregate. In fact, you can use $V_{max}-V(\infty)$ as the activation barrier to estimate the rate at which a colloid aggregates.

Thank you for the answer, but it didn't really answer my question because, as I said in the post, particles can bond in secondary minimum if they can't overcome energy barrier which would still lead to flocculation as bonding occured.

 

[TeethWhitener]

The secondary minimum is almost always quite shallow (on the order of kT). Colloid aggregation in the secondary minimum is therefore pretty easily reversible. The depth of the secondary minimum is dependent on ionic strength. At low ionic strength, the main effect of the secondary minimum is to increase the dwell time of particles nearby each other, thereby indirectly increasing the attempt frequency for incoming particles to surmount the barrier to the primary minimum. At higher ionic strengths, flocculation into the secondary minimum becomes more important.

In the OP, there was one question. The answer to the question is that, thermodynamically, DLVO predicts that colloids are not stable. Kinetically, they can be, usually based on the height of the barrier. In very high ionic strength solutions, the secondary minimum will deepen and the colloids will become less stable to flocculation into the secondary minimum. This is a process sometimes called salting out.

 

[Dario56]

The secondary minimum is almost always quite shallow (on the order of kT). Colloid aggregation in the secondary minimum is therefore pretty easily reversible. The depth of the secondary minimum is dependent on ionic strength. At low ionic strength, the main effect of the secondary minimum is to increase the dwell time of particles nearby each other, thereby indirectly increasing the attempt frequency for incoming particles to surmount the barrier to the primary minimum. At higher ionic strengths, flocculation into the secondary minimum becomes more important.

In the OP, there was one question. The answer to the question is that, thermodynamically, DLVO predicts that colloids are not stable. Kinetically, they can be, usually based on the height of the barrier. In very high ionic strength solutions, the secondary minimum will deepen and the colloids will become less stable to flocculation into the secondary minimum. This is a process sometimes called salting out.

Thank you, I've learned something now. Why is it that increasing ionic strength increases secondary minimum stabilization? I do know that electrolytes affect energy barrier by neutralizing charge of particles, but I didn't know they affect depth of secondary minimum.

 

[TeethWhitener]

Thank you, I've learned something now. Why is it that increasing ionic strength increases secondary minimum stabilization? I do know that electrolytes affect energy barrier by neutralizing charge of particles, but I didn't know they affect depth of secondary minimum.

So, the potential energy curve in DLVO theory is a sum of attractive van der Waals (vdW) forces and repulsive electrostatic forces from the electrical double layer (EDL). Increasing ionic strength of the solution decreases the thickness of the EDL, which means that the repulsive force gets stronger at a shorter distance and weaker at a longer distance. But since the vdW forces don’t change, the total potential ends up with a deeper secondary minimum and a higher barrier to the primary minimum.

 

[shwejaya]

How do we find the maximum and minimum depth of the secondary well in DLVO , I am using varied particle sizes ( eg 40-60 micrometer)