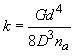Does a Compression Spring's Pitch Affect Its Constant k?

[bobfei]

Hi,

Does a compression spring’s pitch or rise angle have any relation with its spring constant k?
I checked various sources and they differ on this. Some sites simply asks you to feed input into a simple formula:

k=Gd⁴/3D³n_a​

in which

k: spring constant
G: material’s shear modulus
d: diameter of the wire
D: outer diameter of each winding​

An example of this treatment can be found at http://www.efunda.com/DesignStandards/springs/calc_comp_designer_eqn.cfm.

On the other hand, some other sites require knowing the pitch between each winding, or equivalently rise angle θ, and result varies with different pitch/θ even all four parameters above remain unchanged. An example is at http://www.planetspring.com/pages/compression-spring-calculator-coil-calculator.php?id=compression.

I strongly suspect the first type of treatment above is incorrect. Consider extreme case:

1. θ →0° : This means we are not winding the spring up so all windings remains on the same plane. Of course when approaching this extreme k would approach zero.
2.. θ →90°: This corresponding the case when we are pulling the string straight without any winding and it points straight upward. Trying to compressing such a “spring” on the two ends is like compressing a stick rod, and we would get extremely large resistance due
to the rigidity of the material itself. Obviously in this case k → infinity​

It is then quite clear that θ cannot be overlooked, and the first kind of treatment above is obviously wrong.

I wonder why so many websites are still providing that answer? Could someone help or give a derivation of the compression spring k formula?


Bob

 

[AlephZero]

Your first formula includes $n_a$ which is thie number of active coils in the spring. If you change the pitch angle, then for a fixed length of spring you change $n_a$.

Actually the first formula tells you something interesting: for a foxed number of coils, the stiffness does NOT depend on the pitch angle. A "long" spring with 10 coils and a big pitch angle has about the same stiffness as a "short" spring with 10 coils and a small pitch angle.

You can only choose two of the pitch angle, the length of the spring, and the number of coils as independent quantities.

 

[bobfei]

Aleph,

Actually the first formula tells you something interesting: for a foxed number of coils, the stiffness does NOT depend on the pitch angle. A "long" spring with 10 coils and a big pitch angle has about the same stiffness as a "short" spring with 10 coils and a small pitch angle.

This is what I cannot understand: why k(small angle, 10 coils) = k(large angle, 10 coils)? see the below extreme-case reasoning?

1. θ →0° : This means we are not winding the spring up so all windings remains on the same plane. Of course when approaching this extreme k would approach zero.
2.. θ →90°: This corresponding the case when we are pulling the string straight without any winding and it points straight upward. Trying to compressing such a “spring” on the two ends is like compressing a stick rod, and we would get extremely large resistance due
to the rigidity of the material itself. Obviously in this case k → infinity

 

[AlephZero]

Why do you think k approaches 0 when the angle is small? Allowing for the fact that the coils can't intersect each other, when θ → 0 the wire is wound into a spiral. That acts like a curved beam, and its stiffness depends on the length of the wire (i.e. the number of turns).

For a fixed number of turns (and a fixed length of wire), it doesn't make much difference if the angle is exactly 0 or just close to 0.

These simple formulas don't really apply when θ → 90, but for a fixed length of spring, as θ → 90 the number of turns $n_a$ → 0 so the first formula does predict the stiffness gets very large.