Does a Gaussian wave packet remain Gaussian?

[Happiness]

Consider a gaussian wave packet whose wave function at a particular instant of time is

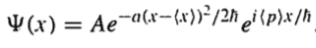
Its time dependence is implicit in the "constants" A, a, <x> and <p>, which may all be functions of time.
But regardless of what functions of time they may be, these constants will take on some values at another instant of time and remain independent of x. So the wave function (at this new time) is still gaussian.
So a gaussian wave packet remains gaussian. True or false?

I think it's false. But what's wrong with the deduction?

 

[mfb]

At the moment you simply assume that the wave function will always have that shape. You have to show that there are functions A(t), a(t), <x>(t), <p>(t) such that the resulting time-dependent wave function solves the Schroedinger equation. The latter two should be quite easy (Ehrenfest theorem), then you can work on a(t).

 

[Happiness]

At the moment you simply assume that the wave function will always have that shape. You have to show that there are functions A(t), a(t), <x>(t), <p>(t) such that the resulting time-dependent wave function solves the Schroedinger equation. The latter two should be quite easy (Ehrenfest theorem), then you can work on a(t).

If the wave packet hits an obstacle, like a potential barrier or a potential well or collide with another wave packet, then it no longer remains gaussian.

But if it is free to move ahead on its own, then it remains gaussian.

True?

 

[mfb]

Don't guess, calculate it.

 

[Happiness]

Don't guess, calculate it.

How do you work on a(t)?

 

[vanhees71]

Hint: It depends on the Hamiltonian! Just think about the question, which class of Hamiltonians $H(x,p,t)$ have a chance to preserve the Gaussian shape (of course with time-dependent parameters, which for a Gaussian are just the average and the standard deviation, as in your ansatz). The hint about Ehrenfest's theorem is also very valuable :-)).