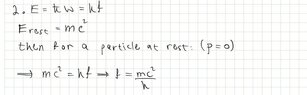E=hf for massive particles, but which Energy exactly?

[AlonZ]

TL;DR Summary

which energy is it in E=hf and in lorentz invariant?

Hi there, I'm a bit confused about the E=hf equation for mass particle(f for frequency), and Lorentz Invariant (E^2 -p^2c^2=m^2c^4).
The question is, which energy is it? Total Energy- Kinetic plus Rest, or only kinetic energy.
Now, if it's total energy, then you get that a particle at rest (Ek=0) has frequency which can't be right by De-Broli's equation p=h/lambda.
And if it's only kinetic energy then I get the following: lambda=h/p=hv/mv^2--> 2Ek=mv^2=hv/lambda=hf (v for speed, f for freq).
so both ways don't add up for me, i have to be wrong somewhere, will be glad for your help.
Thanks a lot.

 

[vanhees71]

In relativistic physics it's always convenient to work with Minkowski scalars, vectors, and tensors. That's why for a free particle you define the energy as you wrote as $E=\sqrt{m^2 c^4+\vec{p}^2 c^2}$, i.e., including rest energy. Correspondingly for the corresponding energy-momentum eigenstates of free particles you have the equation
$$-\hbar^2 \Box \psi(x)=m^2 c^2 \psi(x),$$
where $\psi(x)$ is any kind of relativistic free wave function (Klein-Gordon, Dirac, etc.).

You can of course always redefine the absolute level of energy by an arbitrary constant, i.e., you can use $$E_{\text{kin}}=\sqrt{m^2 c^4+\vec{p}^2 c^2}-mc^2.$$
This then refers to new wave functions only changed by a phase factor $\exp(-\mathrm{i} m c^2 t/\hbar)$ relative to the covariant wave functions defined above. As in classical (relativistic or Newtonian) physics the absolute level of energy is not observable, only energy differences.

 

[Dale]

The question is, which energy is it?

It is total energy.

Now, if it's total energy, then you get that a particle at rest (Ek=0) has frequency which can't be right by De-Broli's equation p=h/lambda.

You have a misunderstanding of de Broglie’s relations. See: https://en.m.wikipedia.org/wiki/Matter_wave

The de Broglie frequency is given by $E=\hbar \omega$ and the de Broglie wavelength is given by $\vec p=\hbar \vec k$ where $\lambda=2\pi/k$. So for a massive particle at rest $p=0$ and $E>0$ so $\lambda = \infty$ and $\omega>0$. I am not sure why you think that is an issue.

 

[AlonZ]

It is total energy.

You have a misunderstanding of de Broglie’s relations. See: https://en.m.wikipedia.org/wiki/Matter_wave

The de Broglie frequency is given by $E=\hbar \omega$ and the de Broglie wavelength is given by $\vec p=\hbar \vec k$ where $\lambda=2\pi/k$. So for a massive particle at rest $p=0$ and $E>0$ so $\lambda = \infty$ and $\omega>0$. I am not sure why you think that is an issue.

What's troubling me is how does a particle at rest has frequency different than 0, as you said w>0.
I'm attaching a file so you can see exactly where my problem is.
if lambda goes to infinity, doesn't frequency has to go to zero? As it does not in the attached photo.
Thanks a lot for the informative replies.

 

[vanhees71]

The plane-wave solution of the Klein-Gordon equation is
$$u_{\vec{p}}(t,\vec{x})=\frac{1}{\sqrt{(2 \pi)^3 2 E_{\vec{p}}}} \exp(-\mathrm{i} E_{\vec{p}} t+\mathrm{i} \vec{p} \cdot \vec{x}),$$
where I use natural units with $\hbar=c=1$. The normalization is chosen in the relativistic covariant convention in QFT. The energy is given by the "on-shell condition",
$$E_{\vec{p}}=\sqrt{\vec{p}^2+m^2},$$
i.e., such that $(p^{\mu})=(E,\vec{p})$ transforms as a four-vector. For $\vec{p}=0$ you get $E_0=m$. There's no problem with that. You can choose the absolute level of the energy as you like without changing any physics, and here it's convenient to choose it in this way such that $(p^{\mu})$ is a four-vector.

 

[Dale]

if lambda goes to infinity, doesn't frequency has to go to zero?

Not in general, no. For a photon $\lambda \omega =c$ so for them it is true that as $\lambda\rightarrow\infty$ we must have $\omega\rightarrow 0$. But massive particles don’t have such a relationship so it isn’t a problem for massive particles. And massless particles can never be at rest so it isn’t a problem for photons either.