MHB Emily's questions at Yahoo Answers regarding a solid of revolution

[MarkFL]

Here is the question:

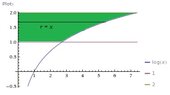
Please help with this simple integral question, thank you?


Write the integral for the volume of the solid obtained by rotating the region bounded by y=lnx, y=1, y=2, and x=0 about the y axis.


THANK YOU SO MUCH!

I have posted a link there to this thread so the OP can see my work.

 

[MarkFL]

Hello Emily,

First, let's plot the region to be revolved:

View attachment 1666

Using the disk method, we may write the volume of an arbitrary disk as follows:

$$dV=\pi r^2\,dy$$

where:

$$y=x=e^y$$

Hence:

$$dV=\pi \left(e^y \right)^2\,dy=\pi e^{2y}\,dy$$

Summing all the disks through integration, we may write:

$$V=\pi\int_1^2 e^{2y}\,dy$$

If we use the substitution:

$$u=2y\,\therefore\,du=2\,dy$$

we may write:

$$V=\frac{\pi}{2}\int_2^4 e^{u}\,du$$

Applying the FTOC, we find:

$$V=\frac{\pi}{2}\left[e^u \right]_2^4=\frac{\pi}{2}\left(e^4-e^2 \right)$$