PhysicsKT
- 17
- 0
The energy density of an electromagnetic field with a linear dielectric is often expressed as
 . It is also known that energy can be found by
. It is also known that energy can be found by
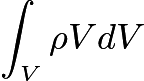 . Using the latter, the energy density is found to be
. Using the latter, the energy density is found to be
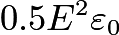 , as is well known. If you integrate the latter only over free charge and ignore bound charge, you write
, as is well known. If you integrate the latter only over free charge and ignore bound charge, you write
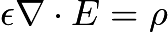 , use integration by parts, and obtain the first result. Does the first result neglect the energy from bound charge? If not, why does
, use integration by parts, and obtain the first result. Does the first result neglect the energy from bound charge? If not, why does
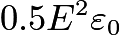 break down (I.e. why can’t one find the energy with a dielectric by treating the bound charge as its own independent charge arrangement and using formulae for a vacuum?)
break down (I.e. why can’t one find the energy with a dielectric by treating the bound charge as its own independent charge arrangement and using formulae for a vacuum?)
Attachments
-
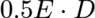 1994848e8909b58aaa7dfa748264681c15b04cdb.png741 bytes · Views: 706
1994848e8909b58aaa7dfa748264681c15b04cdb.png741 bytes · Views: 706 -
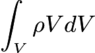 90ce12f273329132bc0a22e77cabd6fadd9317ec.png1,020 bytes · Views: 615
90ce12f273329132bc0a22e77cabd6fadd9317ec.png1,020 bytes · Views: 615 -
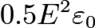 2b95635ceca0346d915aadc5ef5f3f8047d12dd6.png826 bytes · Views: 672
2b95635ceca0346d915aadc5ef5f3f8047d12dd6.png826 bytes · Views: 672 -
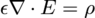 a3e754ebda6b4b4d609f6ac85bb3d8b3f6fa3516.png700 bytes · Views: 556
a3e754ebda6b4b4d609f6ac85bb3d8b3f6fa3516.png700 bytes · Views: 556 -
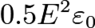 2b95635ceca0346d915aadc5ef5f3f8047d12dd6.png826 bytes · Views: 562
2b95635ceca0346d915aadc5ef5f3f8047d12dd6.png826 bytes · Views: 562