Discussion Overview
The discussion revolves around the unexpected behavior observed when taking the Fast Fourier Transform (FFT) of a conjugate signal in MATLAB. Participants explore why the conjugate of a time-domain signal does not produce an exact flip of the frequency domain spectrum, noting a consistent one-pixel shift in the results.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
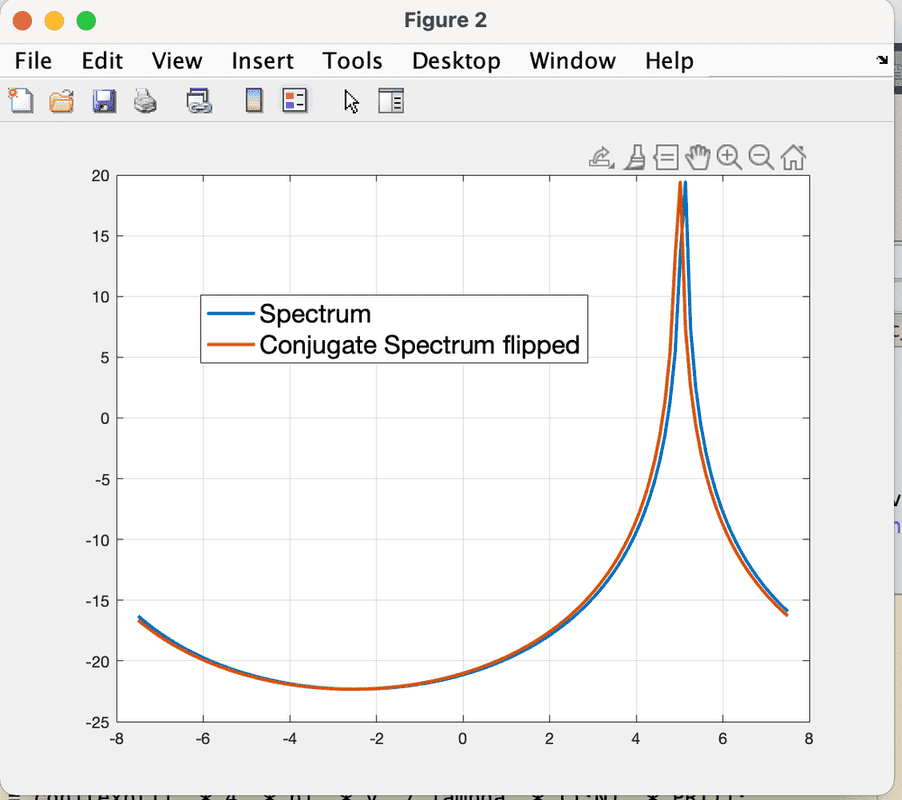
- One participant notes a one-pixel shift in the FFT of the conjugate signal compared to the original spectrum and seeks to understand the cause.
- Another suggests comparing the numerical values of the two curves to determine if they are indeed shifted.
- Some participants propose that the issue may relate to how the graphs are displayed, questioning if overlapping curves could visually misrepresent the shift.
- Concerns are raised about potential rounding errors affecting the results after applying FFT to both the original and conjugate signals.
- One participant identifies that the combination of MATLAB's flip() and fftshift() functions may contribute to the observed shift, particularly regarding the positioning of the zero-frequency value.
- A later reply indicates that the issue may not solely be with the flip function but rather with the definition of the frequency axis used for the FFT.
- Another participant mentions that the peaks of the spectra do not intersect exactly at zero, reinforcing the idea of a consistent offset.
- One participant shares a solution involving a corrected definition of the frequency axis, which resolves the issue of the spectra crossing at the zero velocity point.
Areas of Agreement / Disagreement
Participants express differing views on the source of the one-pixel shift, with some attributing it to MATLAB's functions and others to potential computational errors. The discussion remains unresolved regarding the exact cause of the shift, although a proposed solution has been identified.
Contextual Notes
Participants note that the issue may depend on the specific definitions used for the frequency axis and the behavior of MATLAB functions, which could introduce additional complexity in the analysis.