FFT of conjugate doesn't coincide exactly at the negative frequency

[tworitdash]

I am trying to understand why the conjugate of a signal in the time domain doesn't produce an exact flip of the frequency domain spectrum. There is always a one-pixel shift in the result.

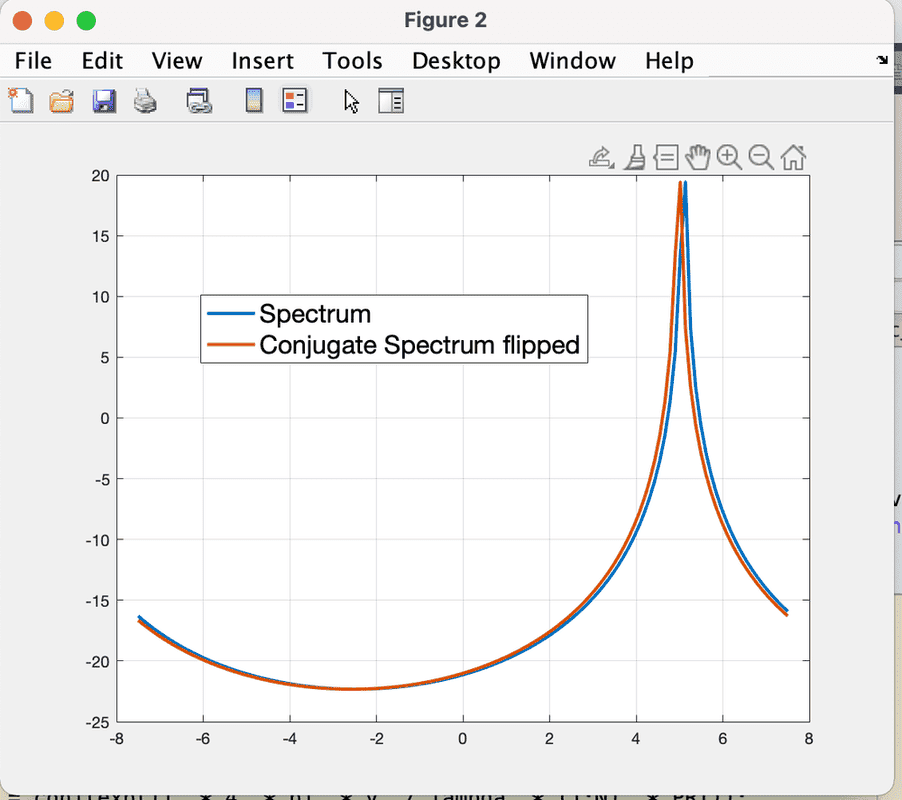
The MATLAB code is shown below. I use a flip for the conjugate spectrum to show that it doesn't match the original spectrum and there is a delay of one resolution cell. I want to understand why this happens. It shouldn't as it is the perfect conjugate.

 

[jedishrfu]

Try comparing the numbers of the two curves to see if they are shifted too.

it could be a graph thing to show that there are two curves vs one curve completely overwriting the other curve.

One could also draw two sin or lines or parabolic curves and see if the graph exhibits the same one pixel shift.

upon resizing the graph is it the same one pixel shift?

 

[BvU]

The code looks very compact to me ..

$\$

 

[tworitdash]

Try comparing the numbers of the two curves to see if they are shifted too.

it could be a graph thing to show that there are two curves vs one curve completely overwriting the other curve.

One could also draw two sin or lines or parabolic curves and see if the graph exhibits the same one pixel shift.

upon resizing the graph is it the same one pixel shift?

The graph has no issue at all. I have tested with Gaussian pulse in the frequency domain as well. It also has the same pixel shift. It is the issue of the conjugate. It shouldn't be like this. Probably something with the DC value which remains in the positive frequency always. I don't know. For simplicity, I used a monochromatic signal here. I usually do it with a Gaussian spectrum.

 

[tworitdash]

The code looks very compact to me ..

$\$

Sorry! Now I can't edit the original post now. So, pasting the code here.

v_max = 7.5;
v = 5;
N = 128;
PRT = 1e-3;
lambda = 0.03;
vel_axis = linspace(-v_max, v_max, N);

x = exp(1j .* 4 .* pi .* v ./ lambda .* (1:N) .* PRT);

x_conj = conj(exp(1j .* 4 .* pi .* v ./ lambda .* (1:N) .* PRT));

x_fft = 1/sqrt(N) .* fftshift(fft(x, N));
x_conj_fft = 1/sqrt(N) .* fftshift(fft(x_conj, N));
figure; plot(vel_axis, db(abs(x_fft)), 'LineWidth', 2); hold on; plot(vel_axis, flip(db(abs(x_conj_fft))), 'LineWidth', 2);grid on;

the original post. So, I am pasting the code here.

 

[jedishrfu]

The reason you couldn't edit your code is due to it not being pasted in the original post that's why @BvU commented on its compactness.

There is a time limit also that comes into play for post editing.

 

[jedishrfu]

Did you compare the data by printing it to see if it's identical?

Rounding error could be happening too.

 

[Office_Shredder]

The graph has no issue at all. I have tested with Gaussian pulse in the frequency domain as well. It also has the same pixel shift. It is the issue of the conjugate. It shouldn't be like this. Probably something with the DC value which remains in the positive frequency always. I don't know. For simplicity, I used a monochromatic signal here. I usually do it with a Gaussian spectrum.

I think their point was, if you draw the same plot twice, does it graphically show them slightly offset just to be helpful.

 

[tworitdash]

I think their point was, if you draw the same plot twice, does it graphically show them slightly offset just to be helpful.

Thank you for clarifying. No, if I use the same plot twice, they perfectly coincide with each other. There is no shift.

 

[tworitdash]

Did you compare the data by printing it to see if it's identical?

Rounding error could be happening too.

In the time domain yes, they both are perfect conjugate. However, after applying FFT to the original and to the conjugate, I see different values indeed.

 

[jedishrfu]

Perhaps this is something you could ask the MATLAB folks about As it seems it may be a subtle flaw in their computational library.

When I said compare the two curves, I meant a point by point comparison to see how significantly different they are. I don’t doubt you that they should be the same but computer math is limited in subtle ways.

If it were a constant x or y difference then you could look to see what is causing it. However, if the difference varies from point to point then that seems to be some other kind of computational issue.

 

[DrGreg]

The problem is the combination of MATLAB's flip() and fftshift() functions.

After fftshift, the zero-frequency value is position 65 in the array indexed 1:128. After you flip, the zero-frequency is in position 64.

 

[jedishrfu]

Great debugging effort there @DrGreg !

 

[tworitdash]

The problem is the combination of MATLAB's flip() and fftshift() functions.

After fftshift, the zero-frequency value is position 65 in the array indexed 1:128. After you flip, the zero-frequency is in position 64.

Thank you for the answer. My problem was indeed not the flip function. I just used flip to see if they coincide and it was indeed a bad choice as you pointed out.

However, my issue was more about the conjugate spectrum. Even without flip, you can see that both the spectra don't intersect each other exactly at 0. Screenshot attached. It is exactly one pixel after 0. That is why their peaks aren't exactly symmetric. You can see the values of abscissa at the peaks in the picture.

I found the fix actually. I was so dumb to use the frequency (velocity) axis wrong for the fftshift. It didn't include the zero frequency point at all. Now I define the axis like this.

Axis = linspace(-N/2, N/2-1, N)/N;
vel_axis = 2 .* v_amb .* Axis;

Now, here you can see the modified one with this velocity axis. They cross each other now at 0 velocity point.