MHB Find Balloon Height: Darshan Amin's Question on Yahoo Answers

[MarkFL]

Here is the question:

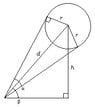
A round balloon of radius r subtends an angle α at the eye of observer while the angle of elevation of its?


A round balloon of radius r subtends an angle α at the eye of observer while the angle of elevation of its centre is β.prove that the height of the centre of the balloon is r*sinβ*cosecα*1/2

I have posted a link there to this thread so the OP can view my work.

 

[MarkFL]

Hello Darshan Amin,

Please consider the following diagram:

View attachment 1804

From this we see:

(1) $$\sin(\beta)=\frac{h}{d}\implies h=d\sin(\beta)$$

(2) $$\sin\left(\frac{\alpha}{2} \right)=\frac{r}{d}\implies d=r\csc\left(\frac{\alpha}{2} \right)$$

Substituting for $d$ from (2) into (1) we obtain:

$$h=r\csc\left(\frac{\alpha}{2} \right)\sin(\beta)=r\sin(\beta) \csc\left(\frac{\alpha}{2} \right)$$

Shown as desired.