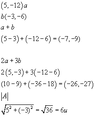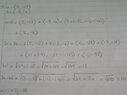Discussion Overview
The discussion revolves around finding the magnitude of the vector difference $\left| a-b \right|$ given the vectors $a$ and $b$. Participants explore vector addition, scalar multiplication, and the application of the Pythagorean theorem in calculating magnitudes. The context includes homework-related queries and technical explanations of vector operations.
Discussion Character
- Homework-related
- Technical explanation
- Debate/contested
Main Points Raised
- One participant initially seeks help with finding $\left| a-b \right|$ after calculating other vector operations.
- Another participant claims to have found the answer to $\left| a-b \right|$ as 10.
- A different participant describes the process of vector addition and scalar multiplication, mentioning the use of the Pythagorean theorem for magnitude calculations.
- One participant expresses confusion regarding the signs in their calculations for $a+b$ and $2a+3b$, indicating a misunderstanding of the operations involved.
- Another participant acknowledges a mistake in their calculations related to the signs and expresses a humorous take on their error.
Areas of Agreement / Disagreement
Participants exhibit some agreement on the general approach to vector operations but also display confusion and disagreement regarding specific calculations and signs in their work. The discussion remains unresolved regarding the correctness of the calculations presented.
Contextual Notes
Some calculations may depend on the correct interpretation of vector components and operations, and there are indications of unresolved misunderstandings regarding signs in the calculations.