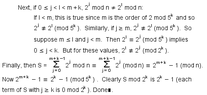Amad27
- 409
- 1
>Let $R$ be the set of all possible remainders when a number of the form $2^n$, $n$ a nonnegative integer, is divided by $1000$. Let $S$ be the sum of all elements in $R$. Find the remainder when $S$ is divided by $1000$.
Here is my working:$2^{\phi(x)} \equiv 1 \pmod{x}$ such that $(2, x) = 1$. So let $x = 125$.
$2^{100} \equiv 1 \pmod{125}$ and consider the cycle that:
$2^{100k + n} \equiv 2^n \pmod{125}$.
$\forall n \ge 3 \implies 2^n \equiv 0 \pmod{8}$.
So I got:
$S = \sum_{k=1}^{99} 2^k = 2^{100} - 1$ but the real answer also considers $2^{100, 101, 102}$ why? $2^{100} \equiv 1 \pmod{125}, 2^{100} \equiv 0 \pmod{8} \implies 2^{100} \equiv 376 \pmod{1000}$.
And then why do they just stop at $102$, what about $103$ etc??
Here is my working:$2^{\phi(x)} \equiv 1 \pmod{x}$ such that $(2, x) = 1$. So let $x = 125$.
$2^{100} \equiv 1 \pmod{125}$ and consider the cycle that:
$2^{100k + n} \equiv 2^n \pmod{125}$.
$\forall n \ge 3 \implies 2^n \equiv 0 \pmod{8}$.
So I got:
$S = \sum_{k=1}^{99} 2^k = 2^{100} - 1$ but the real answer also considers $2^{100, 101, 102}$ why? $2^{100} \equiv 1 \pmod{125}, 2^{100} \equiv 0 \pmod{8} \implies 2^{100} \equiv 376 \pmod{1000}$.
And then why do they just stop at $102$, what about $103$ etc??