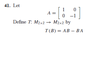charlies1902
- 162
- 0
The problem is attached.
I am instructed to find a basis for the nullspace of T.A basis for a 2x2 matrix is
1 0
0 0
0 1
0 0
0 0
1 0
0 0
0 1Applying the transformation to each of these gives
0 0
0 0
0 2
0 0
0 0
-2 0
0 0
0 0
respectively.
Now this is where I get stuck. How do I find a basis after knowing these 4 matrices?
It look like it's a linear combo of 2 matrices:
0 1
0 0
and
0 0
1 0
but the answer in the book is
1 0
0 0
0 0
0 1
I don't undertand.
I am instructed to find a basis for the nullspace of T.A basis for a 2x2 matrix is
1 0
0 0
0 1
0 0
0 0
1 0
0 0
0 1Applying the transformation to each of these gives
0 0
0 0
0 2
0 0
0 0
-2 0
0 0
0 0
respectively.
Now this is where I get stuck. How do I find a basis after knowing these 4 matrices?
It look like it's a linear combo of 2 matrices:
0 1
0 0
and
0 0
1 0
but the answer in the book is
1 0
0 0
0 0
0 1
I don't undertand.
Attachments
Last edited: