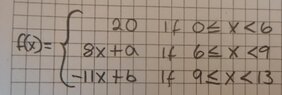SUMMARY
The discussion focuses on finding constants a and b for a piecewise defined function to ensure continuity at x = 6. The correct approach involves setting the limits from both sides equal: $$\lim_{{x}\to{6-}} (20) = \lim_{{x}\to{6+}} (8x+a)$$. This establishes that for the function to be continuous, the left-hand limit must equal the right-hand limit. The participants confirm that this method is valid for determining the constants.
PREREQUISITES
- Understanding of limits in calculus
- Knowledge of piecewise functions
- Familiarity with continuity concepts
- Ability to manipulate algebraic expressions
NEXT STEPS
- Study the properties of limits in calculus
- Explore piecewise function definitions and examples
- Learn about continuity and its implications in calculus
- Practice solving for constants in piecewise functions
USEFUL FOR
Students studying calculus, educators teaching continuity and limits, and anyone working with piecewise defined functions in mathematical analysis.