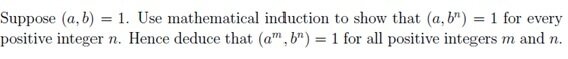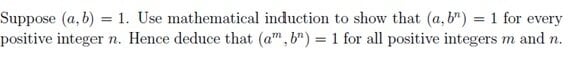GCD Proving Assistance - Get Help Now!
- Context: MHB
- Thread starter Joe20
- Start date
-
- Tags
- Gcd
Click For Summary
SUMMARY
The discussion focuses on proving the greatest common divisor (GCD) condition using mathematical induction. The key points include the necessity of establishing a base case, specifically that for integers \(a\) and \(b\), if \((a,b) = 1\), then \((a,b^n) = 1\) for all positive integers \(n\). Participants emphasize the importance of showing progress in problem-solving to facilitate effective assistance. A technique involving the equation \(ax + by = 1\) is highlighted as a foundational step for the inductive proof.
PREREQUISITES- Understanding of mathematical induction
- Familiarity with GCD concepts and properties
- Basic knowledge of integer equations
- Ability to formulate and manipulate algebraic expressions
- Study the principles of mathematical induction in depth
- Explore GCD properties and their implications in number theory
- Learn techniques for constructing inductive proofs
- Practice solving problems involving GCDs and induction
Mathematics students, educators, and anyone interested in number theory or proof techniques, particularly those focusing on GCD and induction methods.
Similar threads
- · Replies 2 ·
Undergrad
Questions regarding Kurepa's Conjecture
- · Replies 1 ·
- · Replies 19 ·
- · Replies 3 ·
Undergrad
Understanding the Results of gcd(x,n)
- · Replies 8 ·
- · Replies 13 ·
- · Replies 2 ·
- · Replies 2 ·
- · Replies 4 ·