Gear Ratios to Gear Tooth Count

[Mark111]

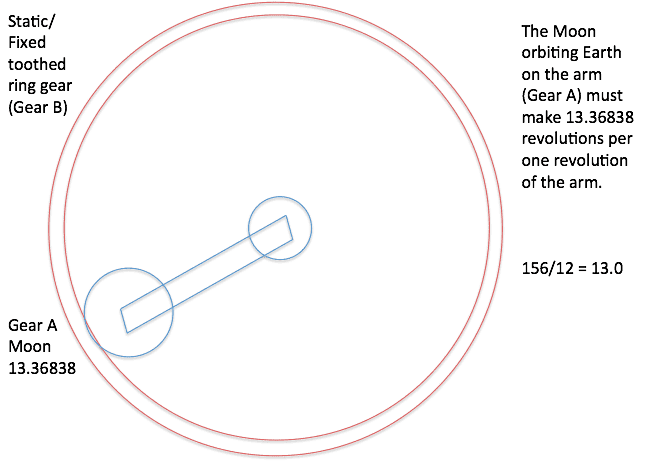
Hello Ladies and Gents,I am look for some help with designing the gear trains for an orrery (a mechanical model of the solar system) I am planning. I need some advice on how to go about calculating the specification of the gears in the mechanism which I will machine. I will use cycloidal teeth I am struggling to understand the relationship between the gear ratio; which I understand to be the "ratio of the angular velocity of the input gear verses the angular velocity of the output gear" and the number of teeth a gear must possesses to honour that ratio. I can’t find a clear explanation of how to determine the appropriate number of teeth a gear must possesses to honour a specific ratio. All of the examples on the Forum have a known number of teeth on one or more of the gears in the train. For example:As in the diagram below; I need the gear that drives the moon (GEAR A) to rotate 13.36838 times per 1 revolution it makes of the fixed ring gear – but how many teeth do I need to reach this outcome. I can guess that 12 teeth on the moon gear and 156 teeth on the fixed ring gear will cause 13.0 revolutions of the moon gear per 1 revolution the arm makes of the fixed ring gear…But this does not get me to the 13.36383 revolutions I need and nor do I find this method repeatable for more complex/less favourable ratios.What is/is there a formulaic method to calculate exact gear ratio into teeth counts?

Many thanks for assistance rendered.

 

[OldEngr63]

The determination of tooth numbers to exactly develop a specified ratio is a tricky subject not deal with in many places at all. It is really quite an art. I can direct you to one (and only one) book that I know of that deals directly with this subject. It is
Mechanics of Machines
by S. Doughty
available from Lulu in a paper back version. This topic is dealt with in some detail on pp. 200 - 209 of that text.

 

[billy_joule]

As in the diagram below; I need the gear that drives the moon (GEAR A) to rotate 13.36838 times per 1 revolution it makes of the fixed ring gear – but how many teeth do I need to reach this outcome. I can guess that 12 teeth on the moon gear and 156 teeth on the fixed ring gear will cause 13.0 revolutions of the moon gear per 1 revolution the arm makes of the fixed ring gear…But this does not get me to the 13.36383 revolutions I need and nor do I find this method repeatable for more complex/less favourable ratios.

you know that 156/12 = 13

you need to solve x/y = 13.36838
where x and y are the smallest integer solution.

Unfortunately, your moon gear will require fifty thousand teeth...

http://www.wolframalpha.com/input/?i=13.36838+rationalize

 

[Mark111]

Thanks for the replies chaps. I see from the rationalization that it is very hard in practice to make accurate systems that are practically machinable. I take it people have always just dealt with this error in clockwork mechanism or designed units of measure that divide rationally into one another.

As a thought, and your feedback welcome - would using pulleys and belts be a more accurate way to achieve finer scale measurements (albeit in low torque applications). I'm thinking that the circumference of the pulley could be an infinitely finer scale (as fine as the resolution of ones equipment) and would allow for non interger ratios that would otherwise restrict one when using toothed gears?

Many thanks also for the reference to Doughty. Will follow that up as no doubt a useful text.

Cheers.

 

[SteamKing]

This article describes how an Orrery can be constructed from a Meccano set (or an Erector set for US readers).

http://www.sis.org.uk/bulletin/94/meccano.pdf

The details of construction give the specification of the gears required to simulate the orbits of the planets (there are quite a few gears involved).

 

[Dr.D]

The solution proposed by Billy_Joule is based on the assumption of a single gear pair. A much better approach is to several compound pairs, which allows you to come much closer with realistic tooth numbers. It may still not be possible to exactly hit the required ratio, but it should be possible to be quite close.

 

[jack action]

If we try the solutions proposed by Dr. D and billy_joule, you can define a set of «correcting» gears, with an exact ratio of 13/12, for example. That means that your gear ratio needed is now 13.36838 / (13/12) = 12.340043. Putting 12.34 in Wolfram, you get a ratio of 617/50.

So combining both ratios, we get 617/50 * 13/12 = 13.3683333333 or a -0.000349 % error.

You play around with different sets of «correcting» gears (14/13, 15/14, 16/15, ...) and when you get to 20/19, you find out that you need a ratio of 12,699961 (or 12.7) which can be obtained with the ratio 127/10. 127/10 * 20/19 = 13.36842105... which has an even slightly less error (+0.000307 %) than the previous set. But more importantly, 127/10 = 254/20 and 254/20 * 20/19 = 254/19 ! So only one gear set needed !

The fun is to play around with these numbers until you have the precision desired. You can also add multiple sets of «correcting» gears.

 

[OldEngr63]

Jack, are you proposing a single stage with 254 teeth on the gear? I don't think that will work out too well. Please let me know who is going to cut that gear for you.

 

[Mark111]

The principal of correcting ratios is very cleaver. I think 254 teeth might be pushing it a bit. Can this principal be applied to compound gear trains and if so would you be kind enough to show a worker example?

How would one add multiple sets of correcting gears As you suggest?

 

[jack action]

​

 

[Mark111]

Hi Jack,

So when you developed the 127/10 which is a ratio of 12.7 and multiplied it by 20/19 which is 1.05263 to get 13.3634 what does this do to the gear train in real terms?

Is there now a 127 toothed gear meshed to a 10 toothed gear and then a 20 tooth gear on the same shaft as the 10 toothed gear, the 20 tooth gear then meshes a 19 tooth gear on a separate shaft?

 

[jack action]

Is there now a 127 toothed gear meshed to a 10 toothed gear and then a 20 tooth gear on the same shaft as the 10 toothed gear, the 20 tooth gear then meshes a 19 tooth gear on a separate shaft?

Yes, exactly.

Here's one with 3 gear sets, each with a ratio of 3:1 (or 1:3, depending on which end is driven). Total gear ratio is 3 * 3 * 3 = 27:1 (or 1:27):

​

 

[Mark111]

Thanks again Jack, unfortunately this is sinking in quite slowly with me and I have another question related to the above example where we have the 127:10 and 20:19 compound gear chain giving us the desired 13.36 ratio.

Let's imagine for whatever practical reason that a 127 tooth gear is to large (it likey is not, but I'm bound to run into this problem soon or later). So is it possible to turn the 127:10 into a compound gear train that can drive the 20:19 at same ratio of 12.70 (that being 127/10 driving 20/19 giving the overall 13.36)? The output gear of the complete compound train (if correctly calculated) should be turning 13.36 times faster than the input or vice versa depending on the driven-driver - correct?

If the above statement is correct the I can go about making a compound gear train with a 12.7 :1 ratio, but 127/10 has no (useful) commonly divisible values to give whole integers - I think only 1 is common.

So to make a ratio of 12.70 do I apply the same method as we discussed early (correction gear)?

127/10 = 12.7

12.7/(e.g.13/12)= 11.72 = 293/25

(293/25)* (13/12) = 12.7 (ended up with a larger gear than I started with)

Neither 293/25 nor 127/10 can be simplified so with no common divisible factors I can't see how to get a smaller compound drive train to reduce the practical size of the 127 toothed gear.

I'm probably confusing myself here but any lead from here would be great,

 

[jack action]

First, I'm no expert in gear making. It is just a fun math problem for me to solve. You should take a new look at the first video I posted about the wooden gears for a clock, it is very instructive.

Now here is how you can apply it to your problem.

To get the smallest ratios you have to use the roots. For example, for 2 gear sets, each set must have a ratio of 3.6562795... [= (13.36838)^(1/2)]. For 3 gear sets, each set must have a ratio of 2.373338... [= (13.36838)^(1/3)]. And so on. Note that the more gear sets you have, the smaller is your «average» ratio, so less difference in the number of teeth between the driver and the driven gears.

But all of these won't give round numbers since you don't start with one to begin with. So let's say you are satisfied with a ratio of approx 3.6562795. Choose the first «round» ratio below that, say, 3.5. This is 7/2 = 14/4 = 28/8 = 56/16, depending on what you think your minimum number of teeth should be.

Now the second gear set should be 13.36838 / 3.5 = 3.819537. Again not a round number. Again we take a lower ratio than this one, say, 3.6666666. This is 11/3 = 22/6 = 44/12. The gear set ratio that is left is 13.36838 / 3.5 / (11/3) = 1.04169... This is our «correcting» gear set ratio. Multiply that ratio with different number of teeth (12, 13, 14, etc.) and you find out that when multiplied by 24 it gives 25.00061 teeth needed to achieved that ratio.

So 56/16 * 44/12 * 25/24 = 13.3680555555... or an error of -0.0024 %. If that is not enough precision for you, you can always play around with other ratios.

 

[Mark111]

Thanks very much for taking the time to reply in such detail jack, you're obviously a very proficient mathematician - I on the other hand am a bit slow with picking it up especially concept that are Not as formulaic in approaches as perhaps any area such as mechanics. Let me work thought the example above and try it with some other numbers and let you know how I go. I hope you won't mind if I drop back with some questions on this

 

[OldEngr63]

I don't have a good understanding of the application for this gear train, so let me simply make a couple of general comments.

1. In making wooden gears, you can be somewhat sloppy; why not? You cannot form the wooden teeth with great precision anyway. If you want real precision in the resulting motion, you cannot play quite as fast and loose with the center distance as Matthias does in his video. The more you open up the center distance, the lower the contact ratio goes. A contact ratio significantly greater than 1.0 is necessary simply to assure that there is always at least one tooth pair engage. Without that assurance, there will be points in the motion when there are no tooth pairs engaged. Also, lowering the contact ratio will make for a more noisy gear set (but for wooden gears, who cares?).

2. According to the AGMA, to avoid undercutting on the teeth, the pinion must have at least 18 teeth for a 20 deg pressure angle and 12 teeth for a 25 deg pressure angle. Thus a 10 tooth pinion is assured to undercut. This will (1) weaken the tooth, and (2) result in non-involute action at points in the motion.

Will wooden gears work for this application, or do you need precision cut metal gears? I don't know, but you need to be aware of these potential pitfalls.

 

[Mark111]

Great additional information OldEng63, that really helps me with the finer design considerations. I'll just summarise a couple of things for you information and fire off some questions that result. So firstly;

I'm planning to CNC the gears on a Sherline lathe/mill system out of 3.175mm (or 1/8" in old money) thick brass sheet so, obviously hoping for very little play and an accurate mechanism.

I'm aiming to use a cycloidal tooth profile, which research has lead me to believe can tolerate a higher pressure angle that results from smaller circumference/less teeth - does that fit with your knowledge?

I wasn't planning to producing cycloidal gears with less than 18 teeth (although I think I can get away with a 12 tooth cycloidal); Where less than 18 teeth are requiring I was going to fabricate a lantern gear out of two brass end plates and thin steel bar stock (~<1mm dia) connecting them - I think the lantern gear can cope with both the increased pressure angle and otherwise reduced contact ratio?

The centre to centre distance and resulting contact ratio is not something I've studied in detail yet, but I understand this to refer to a ratio that represents the average number of teeth of two meshed gears in contact at anyone time. So essentially the more gear teeth are meshed the smoother and more reliable the systems is?

So could it be said that having two gears meshed with 25 teeth and 24 teeth would produce a higher contact ratio that 10 teeth meshed with 150 teeth?

 

[Dr.D]

One of the fundamental requirements for a satisfactory gear pair is that the angular velocity ratio be constant. If this is not met, with the driving gear turning at constant speed, the driven gear with speed up and slow down repeatedly as the teeth go through engagement. This makes for noise and for torsional vibration in the gear train.

The spoke and lantern pair does not have a constant velocity ratio.

Cycloidal gears have a constant velocity ratio only when mounted on exactly the correct center distance. This is a difficult criterion to meet, and gives you no leeway in the shaft center distance assignment. Cycloidal gears are virtually unheard of outside the watch and clock industry, and for good reason. Involute gears have many advantages, and I would certainly urge you to go with the involute profile.

It seems that you are demonstrating why gear train design is usually left to folks who have studied it in considerable detail and know a lot about the subject.

 

[jack action]

Before you go too deep into gear design, remember that most of the theory out there is for making gears that can transmit large loads and/or high-precision positioning and/or minimal wear and/or minimal noise. But if you are making a simple toy (no offense), where only relative positioning of two shafts is of importance, you can be a lot looser on the criteria. IMHO, you could simply used cage gear and it would be fine. Otherwise, it can get crazy and if you are not math-oriented, you won't like it. Here's an equation for contact ratio (http://psas.pdx.edu/lv2cguidance/contact_ratio/ ):

http://psas.pdx.edu/lv2cguidance/contact_ratio/fcc0c10c2303e33528223039a2453320.png

For more info on gear design, I like http://www.thegears.org/spur-and-helical-gears-for-parallel-shafts-design-theory/ and you got some good stuff here too.

 

[Dr.D]

Or, for that matter, for a toy perhaps just use frictions wheels and forget about tooth forms altogether.

 

[Mark111]

Jack I’ve been working through the methods you set out in your post yesterday and this technique works amazingly well. I’ve been able to identify multiply combinations of favorable gear sets to drive the motion of the inner planets and moon of Earth to the desired accuracy. I had to set up a matrix of sorts in Excel to help me spot the factorization and also speed the selection of the correcting gear set ratio, but it’s done the trick! Really great practical advice and well explained, thanks so much.

Dr D thanks also for the insight into gear tooth profiles and associated parameters. I am aware of the limited contemporary use of cycloidal gear profiles, save horology, but remember a orrery is essentially an astronomical clock, albeit a relative one. I was drawn to the cycloidal gears on the basis of the larger reductions they can facilitate compared with involuted gears; similarly I understand a cycloidal gear is less likely to undercut for a smaller given number of teeth (?). Also I’m seeing that cycloidal gears are more adept at functioning without lubrication and typically run with less friction. As Jack also points out there will not be significant amounts for force being transmitted through the gear train. I’m planning to centre gears on 1/8” steel shafts with milling to 0.001” so hoping centre to centre distance should not cause me strife. The issue with centre distance only causes problems when there is play in the gear mount right? So if the addendum and dedendum arcs are correct (allowing enough clearance - the BS 987 (see below) suggests using 95% of the theoretical addendum height to account for machining tolerance and centre to centre diameter shift) there should be a constant velocity ratio between cycloid all gear pairs?

Never the less I’ve been working on ascertaining the contact ratios and my understanding thus far is that as long as the contact ratio is > 1 in the worst case, then the angular velocity should be constant between the two gears (?).I’ve been basing my calculations and design of cycloidal gears on an article by Hugh Sparks (2013) which draws from the British Standard for Cycloidal gears (BS:978). Sparks does a very good job of explaining the design consideration and associated calculations of colloidal gears in plain terms - very useful piece of work.

 

[OldEngr63]

There are two parts to the center distance problem:

1) There is the error due to machining inaccuracies -- this can be managed by careful machine work.

2) There is the situation where we would like to deliberately open up center distance in order to achieve desired shaft center line positions -- this can be easily done with involute gears, but is not tolerated at all by cycloidal gears.

 

[scientific601]

Sorry to arrive late to the party.
I did not find this particular blog back in March... I was certainly looking for any questions to try and see if there was sufficient interest in this topic. Plus during February, March and April I was busy fine tuning my proposed gear calculator. This was my first major project to implement while learning JavaScript.

Unfortunately there is no formulaic method to convert an arbitrary ratio to gear train teeth numbers. Mathematically, the process of determining gears is labour intensive. It belongs to the class of problems of NP-hard computational complexity. That is, no shortcut equation exists that can churn out solutions.

Around 150 years ago French clockmakers formalized the finding of arbitrary fractions by using a Stern-Brocot tree. This is a structured approach to finding fractions which are close to any desired number eliminating hours of guesswork. Another related method is the use of continued fractions.

The subsequent factoring process of such fractions into usable gear tooth counts would then be applied. There were no clever techniques to speed that part up.

It seems that even in today's scholarly machinist's textbooks, this is as far as they go. The factoring part - choosing the gear teeth numbers is ultimately a trial and error exercise after a number of candidate rationals have been found.

I was determined to find a solution that's practical on today's computers. By "practical" I mean that it should do the calculations reasonably quickly for 2, 3, or even 4-stage gear trains.

I believe I have achieved a workable gear train calculator. Possibly the first of its kind on the internet.

See Gear Train Calculator
For the example for ratio 13.36838 it recommends gears 31:71,22:59,17:37 which gives a ratio accurate to 6 decimal places: 13.36838019665344
Mark111's original post did suggest a planetary gear arrangement... so the ratio might have to be modified as the arm's rotation adds another full rotation to the planet gear as I understand it.

Although late to this particular thread, I hope that it can be useful for gear problems others may encounter. It's free. I'm not selling or pushing anything. Optimizations, algorithms, "difficult" problems is my hobby.

I'm just a retired dinosaur programmer that's putting his skills to good use instead of evil. :)

 

[Dr.D]

That is a very interesting program, and you are most certainly correct about the difficulty of the problem. Have you (or do you plan) to publish your approach? I would be very interested in knowing more details about how you solved this problem.

 

[scientific601]

Thanks for your interest.
I could certainly go into how I "solved" the problem.
Not sure if this is the appropriate thread to do that in... Maybe a new thread? Or on my site I could put up a "theory" page.

 

[scientific601]

The tone of this thread includes some theoretical approaches already so perhaps it's OK if I post the method here.

Compound Gear Train Calculations

Let's say we wanted to achieve a ratio of 13.36838 from the OP's example.

We want to find the gear sizes required to produce an overall speed ratio of R. Let's settle on a three stage gear train for this. A 2-stage would only achieve 3 digit accuracy at best.

In non-gear speak we are looking for three fractions whose product is R. Or as close to R as requested. As well, all numerators and denominators must not be greater than 100. There was no minimum number specified in the problem but a practical gear minimum is 12 teeth (involute profile, pressure angle $20^\circ$).
$$ \left ( \frac {b} {a} \right ) \left ( \frac {d} {c} \right ) \left ( \frac {f} {e} \right ) = R \ (13.36838) $$
There is one equation and six (6) unknowns: a, b, c, d, e, f. These represent the number of teeth on six gears. Each of these integers is limited to a range of 12 to 100.

Frankly my math skills are not sufficient to consider Diophantine equations which may offer some beneficial lower and upper bounds to our problem. Also it's not at all clear whether we should pursue the more abstract math branches such as related Prime Factorization, B-smooth Numbers, and offline Bin-Packing.

So instead let's barge ahead with an implementable computer programmable solution.

Brute-force attack

If one proceeds with an impulsive brute-force method, one is faced with a huge number of permutations. Each of the six gears can have 89 sizes (100 - 12 + 1)
$$ 89^6 = 496,981,290,961 $$
Nearly four hundred ninety-seven billion! Trying out all permutations to see which one comes closest to the desired result would take a computer from a few hours to a few days of computing time.

That method is already impractical and would become more so for higher number of gears. Adding one more stage would multiply the above computations by 7921 ($89^2$). Now we'd be facing years or even decades of computing time.

It should be intuitively obvious that churning through all possible permutations of gear sizes is extremely wasteful. There is no interaction of gears assumed. In other words, partially calculated ratios from some of the gears does not narrow the search field for the remaining gears even though it's logical that they should.

We are forced to evaluate billions of impossible ratios that are given an 'equal' chance at success. Not to mention the millions of duplicate ratios that the six gears' interchangeability generate.

If you are told that a target is hanging on one wall and you are led to this room blindfolded, is it sensible to throw billions of darts in every direction including the floor and ceiling?

A Faster Method

Fortunately the Gear Train Calculator performs the calculation in much less time. It does not try out all permutations in the manner suggested. Instead it attempts to factor only candidate rationals $\frac {B}{A}$ which are close to the desired ratio. Remember that a rational number is a fraction (composed of integer numerator and denominator).

Our six gear sizes a,b,c,d,e,f are combined rather than treated separately.
$$ \frac {B}{A} = \left ( \frac {b \times d \times f }{a \times c \times e } \right ) $$
This may seem like a trivial distinction from the previous brute-force approach. However, we are now considering only a single fraction $\frac {B}{A}$ whose numerator and denominator need to be factorable into three factors each. The number of permutations that need to be considered are now dramatically reduced.

If gears a, c, e (the denominators) are all at their minimum size then A is minimized:
A's minimum value is $12^3 = 1,728$
The largest that A can get when B is maximized: $\frac {100^3}{13.36838} = 74,803$

Therefore A can range from 1,728 to 74,803. This means we will test 73,076 fractions. A lot less than 497 billion. A nearly seven million factor speedup.

The numerator B is always $A \times 13.36838$, rounded to the nearest integer. We divide out that fraction to check how close it is to that ratio. If the result is fairly close (for example, closer than a previous estimate) then we try to factor B and A into three factors each that satisfy our teeth range limits. Factoring consists of a linear search for divisibility, done recursively for subsequent stages. However there are optimizations possible for factoring odd numbers as well as dynamically narrowing search ranges.

It turns out that the best fraction $\frac {B}{A}$ whose numerator and denominator is factorable into 3 factors each is $\frac {154993}{11594}$

For the final result this best ratio $\frac {B}{A}$ is re-factored to find the optimum gears. This time all possible factorizations are evaluated rather than stopping at the first possible one as was done above. It is desirable to get the lowest total tooth count. At least that's what I assumed gear hobbers would like. Therefore factorizations are favoured where the sum of $b + d + f$ is minimized as well as the sum $a + c + e$.

The final step is to present the gear sizes in order - largest to smallest. This comes out naturally from the direction of the factorization flow so a sort was not necessary.

Optimum result:
31:71,22:59,17:37

In this result as in any result, odd-positioned numbers may be interchanged with other odd-positioned numbers. Similarly even-positioned gears may be exchanged with other even-positioned gears. This does not affect the ratio since all we are doing is shuffling the numerators or denominators amongst themselves.

The result can be interpreted as:
$$ \frac {71}{31} \times \frac {59}{22} \times \frac {37}{17} = 13.36838019665344 $$
Summary thoughts

The method described reduces the search for compound gear train teeth counts by a substantial amount compared with an exhaustive random gear permutation search. It does this by focusing only on 'close' approximations to the desired ratio. While it's still a labour intensive exhaustive search, the order of complexity is minimized.

The method is still not practical enough to be hand-calculable. Such is not possible given the class of this mathematical problem. Students of mechanical engineering will need to continue to use established methods to approximate ratios and the necessary multiple attempts to factor them and to show their work! It is however clear that unless a decidedly exhaustive search is undertaken, or the use of computer solutions such as the one here, their solutions will not be guaranteed to be optimal.

The Gear Train Calculator can also perform reverted gear train solutions. The method for that function are considerably different than the one described here so far.

 

[OldEngr63]

Very interesting write-up. I hope that you will do something similar for the reverted gear train design.

Just a very small quibble here.

Back in the 1980s when I was much more concerned with these matters, the AGMA standard for involute gear teeth said the following regarding the minimum number of teeth on a pinion:
20 deg Coarse Pitch -- min number of teeth = 18
25 deg Coarse Pitch -- min number of teeth = 12
20 deg Fine Pitch -- min number of teeth = 10
I would expect these min values to still apply since I cannot see that anything has changed to make things different.

 

[scientific601]

Yes you are right. I was probably looking it up for 25 degree by mistake - just to get a quick number. Even the maximum of 100 is probably not realistic to make for home machinists. However in this particular example the maximum teeth count required was 71.

Any teeth count limits can be tried in the calculator from 3 to 400. It's interesting to see how the final result is affected. Choosing a more restrictive range will result in ratios with greater error from the desired ratio. Sometimes the total number of teeth is greatly reduced with just a small penalty of increased error. This may be desirable for manufacturing ease.

I could do a writeup of my method of calculating gears for a reverted train design. Again it will be in the form of an algorithmic approach. The assumption is that a computer is the intended tool of choice.

I'm frankly surprised that there is so little available to take gear train calculations out of the dark ages. Perhaps the horologists want to keep it a black art on purpose. I mean, we have tons of good programmers and mathematicians. Perhaps the disciplines rarely intersect.

The Guinness Book of World Records has recently inducted a watch company for their "most precise lunar phase wristwatch".
Hmmmm, the ratios could be worked out in 0.02 seconds (0.25 seconds on my iPhone).
Ratio 118.1223554124 (synodic month x 4 for a 2x moon display driven from an hour hand) gives a 3-stage gear train:
67:93,13:88,7:88. These gears produce an error of 1 day in over 2 million years just like the watch.
Maybe I'm missing something. Or maybe I should win the Nobel Prize.

 

[OldEngr63]

I'm frankly surprised that there is so little available to take gear train calculations out of the dark ages.

Much of what you have done is described in Mechanics of Machines by Doughty (Wiley, 1988, Lulu, 200x), although the full computer algorithm is not developed there. This seems to have been a bit of an anomaly at that time, and remains so today. As far as I can tell, the attitude of most engineers in most situations is along the lines, "We have to slow it down (speed it up) by about a factor of x," but hitting the exact ratio is not often considered critical. The clock/watch case is obviously an exception, and I think on the whole, we could do better engineering if we would but try. I think your work here is a very significant contribution, and you are to be congratulated. Please do write up the reverted train design process.

 

[scientific601]

OK here goes. This is more like a math / algebra / computer algorithm lesson rather than physics and gearing... but like I said, these disciplines happen to intersect in gear design as far as I can see.

Reverted Gear Train Algorithm

A reverted gear train is one where the input and output shafts are collinear. Usually what is implied is a 2-stage gear train. Examples are clocks whose hour and minute hand rotate around a "common" shaft - although they are actually on separate shafts that are nested one inside the other. Many transmissions are designed to have their output shaft in line with the input shaft. Yet those shafts are at opposite ends of the casing. This too satisfies the requirement for a collinear arrangement.

What it means mathematically is that the distance of the centers of the first gear pair is equal to the distance in the second gear pair. Or put another way, the teeth count totals of the pairs must be equal.

So not only do we have to meet the requirement:
$$\tag{1} \left( \frac {B}{A} \right) \left( \frac {D}{C} \right) = R \ \text {(Standard 2-stage gear train)}$$
Also collinear axes arrangement is maintained by
$$\tag{2} A+B=C+D$$
The restriction is enforced by the module or diametrical pitch being equal on all gears. Otherwise a regular 2-stage gear train would suffice where the pairs of gears simply have different pitches to comply with their center distances matching.

Again as in the compound gear train example we seem to be faced with too many unknowns. The second formula is just a filter. If our teeth range is 10 to 110, leaving a latitude of roughly 100 possibilities per gear, then the permutations would amount to $100^4=100,000,000$. This is not astronomical for today's computers to process but it can be greatly reduced.

Eliminate variables

Let's reduce the degrees of freedom. We can eliminate variables C and D by combining those two formulas.

From equation (2) we know $D=A+B-C$

Therefore from equation (1) $\frac{D}{C}$ can be replaced with $\frac{A+B-C}{C}$

The value of this fraction can be gleaned from A, B and R.

Let's go through elimination and simplification.

$R\times \frac{A}{B}=\frac{A+B-C}{C}$

$R\times \frac{A}{B}=\frac{A+B}{C}-1$

$R\times \frac{A}{B}+1=\frac{A+B}{C}$

$\therefore \tag{3} C=\lVert \frac{A+B}{R \times \frac{A}{B}+1} \rVert \ \text{(Vertical bars denote "rounding".})$

We resign ourselves to needing A and B to traverse the entire possible gear teeth range. By having eliminated C and D from our search space our permutations have been reduced from 100 million down to $100^2=10,000$.

We can see that C and D are inferred and thus need not have their own permutation generating loops. Also, since there are minimum and maximum limits on the gear sizes, we can "early out" during some searches. For example we can determine that for certain A that B may be out of range always thus making A's initial guess invalid. So ultimately we reduce the 10,000 further, it being the worst case. It turns out that for ratios more distant from 1 the number of tries is reduced the most.

The rest is brute force

What remains is an exhaustive search within a very manageable complexity. We simply go through all A and B systematically checking each fraction multiplied by the (D/C) part that they dictate. We are guaranteed each attempt complies with the reverted gear train requirements thanks to formula (3). We keep track of the closest ratio so far and keep crunching to the end.

The Gear Train Calculator manipulates the final result so that the idler compound gear (represented by the inner two numbers) will contain the lower numbered largest gear. There is no pressing reason for this but just something extra I threw in thinking that this may be desirable.

For a ratio of 12 for example - a very common requirement in clocks as was stated at the outset, the calculator produces 10:30,8:32
Note that 10+30 = 8+32

I believe the calculator is the only one on the internet that does reverted gear trains.

None of the math techniques are groundbreaking in the reverted nor the compound gear portion. It's just that no one else has put together a finished tool that puts theory into practice.