The tone of this thread includes some theoretical approaches already so perhaps it's OK if I post the method here.
Compound Gear Train Calculations
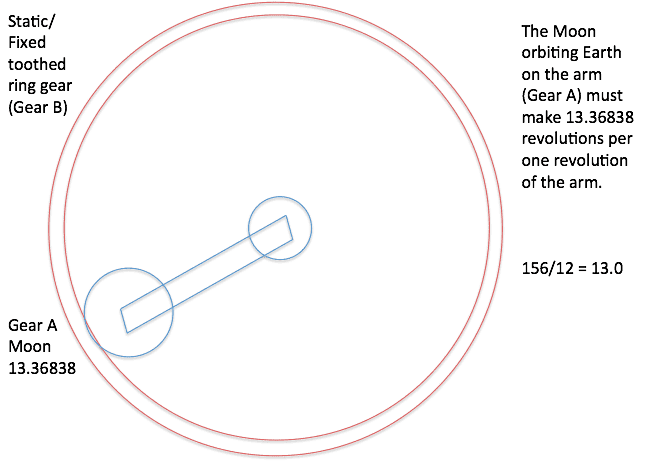
Let's say we wanted to achieve a ratio of 13.36838 from the OP's example.
We want to find the gear sizes required to produce an overall speed ratio of R. Let's settle on a three stage gear train for this. A 2-stage would only achieve 3 digit accuracy at best.
In non-gear speak we are looking for three fractions whose product is R. Or as close to R as requested. As well, all numerators and denominators must not be greater than 100. There was no minimum number specified in the problem but a practical gear minimum is 12 teeth (involute profile, pressure angle ## 20^\circ ##).
$$ \left ( \frac {b} {a} \right ) \left ( \frac {d} {c} \right ) \left ( \frac {f} {e} \right ) = R \ (13.36838) $$
There is one equation and six (6) unknowns: a, b, c, d, e, f. These represent the number of teeth on six gears. Each of these integers is limited to a range of 12 to 100.
Frankly my math skills are not sufficient to consider
Diophantine equations which may offer some beneficial lower and upper bounds to our problem. Also it's not at all clear whether we should pursue the more abstract math branches such as related Prime Factorization, B-smooth Numbers, and offline Bin-Packing.
So instead let's barge ahead with an implementable computer programmable solution.
Brute-force attack
If one proceeds with an impulsive brute-force method, one is faced with a huge number of permutations. Each of the six gears can have 89 sizes (100 - 12 + 1)
$$ 89^6 = 496,981,290,961 $$
Nearly four hundred ninety-seven billion! Trying out all permutations to see which one comes closest to the desired result would take a computer from a few hours to a few days of computing time.
That method is already impractical and would become more so for higher number of gears. Adding one more stage would multiply the above computations by 7921 (##89^2##). Now we'd be facing years or even decades of computing time.
It should be intuitively obvious that churning through all possible permutations of gear sizes is extremely wasteful. There is no interaction of gears assumed. In other words, partially calculated ratios from some of the gears does not narrow the search field for the remaining gears even though it's logical that they should.
We are forced to evaluate billions of impossible ratios that are given an 'equal' chance at success. Not to mention the millions of duplicate ratios that the six gears' interchangeability generate.
If you are told that a target is hanging on one wall and you are led to this room blindfolded, is it sensible to throw billions of darts in every direction including the floor and ceiling?
A Faster Method
Fortunately the
Gear Train Calculator performs the calculation in much less time. It does not try out all permutations in the manner suggested. Instead it attempts to factor only candidate rationals ## \frac {B}{A} ## which are close to the desired ratio. Remember that a rational number is a fraction (composed of integer numerator and denominator).
Our six gear sizes a,b,c,d,e,f are combined rather than treated separately.
$$ \frac {B}{A} = \left ( \frac {b \times d \times f }{a \times c \times e } \right ) $$
This may seem like a trivial distinction from the previous brute-force approach. However, we are now considering only a single fraction ## \frac {B}{A} ## whose numerator and denominator need to be factorable into three factors each. The number of permutations that need to be considered are now dramatically reduced.
If gears a, c, e (the denominators) are all at their minimum size then A is minimized:
A's minimum value is ## 12^3 = 1,728 ##
The largest that A can get when B is maximized: ## \frac {100^3}{13.36838} = 74,803 ##
Therefore A can range from 1,728 to 74,803. This means we will test 73,076 fractions. A lot less than 497 billion. A nearly seven million factor speedup.
The numerator B is always ## A \times 13.36838 ##, rounded to the nearest integer. We divide out that fraction to check how close it is to that ratio. If the result is fairly close (for example, closer than a previous estimate) then we try to factor B and A into three factors each that satisfy our teeth range limits. Factoring consists of a linear search for divisibility, done recursively for subsequent stages. However there are optimizations possible for factoring odd numbers as well as dynamically narrowing search ranges.
It turns out that the best fraction ## \frac {B}{A} ## whose numerator and denominator is factorable into 3 factors each is ## \frac {154993}{11594} ##
For the final result this best ratio ## \frac {B}{A} ## is re-factored to find the optimum gears. This time all possible factorizations are evaluated rather than stopping at the first possible one as was done above. It is desirable to get the lowest total tooth count. At least that's what I assumed gear hobbers would like. Therefore factorizations are favoured where the sum of ## b + d + f ## is minimized as well as the sum ## a + c + e ##.
The final step is to present the gear sizes in order - largest to smallest. This comes out naturally from the direction of the factorization flow so a sort was not necessary.
Optimum result:
31:71,22:59,17:37
In this result as in any result, odd-positioned numbers may be interchanged with other odd-positioned numbers. Similarly even-positioned gears may be exchanged with other even-positioned gears. This does not affect the ratio since all we are doing is shuffling the numerators or denominators amongst themselves.
The result can be interpreted as:
$$ \frac {71}{31} \times \frac {59}{22} \times \frac {37}{17} = 13.36838019665344 $$
Summary thoughts
The method described reduces the search for compound gear train teeth counts by a substantial amount compared with an exhaustive random gear permutation search. It does this by focusing only on 'close' approximations to the desired ratio. While it's still a labour intensive exhaustive search, the order of complexity is minimized.
The method is still not practical enough to be hand-calculable. Such is not possible given the class of this mathematical problem. Students of mechanical engineering will need to continue to use established methods to approximate ratios and the necessary multiple attempts to factor them and to show their work! It is however clear that unless a decidedly exhaustive search is undertaken, or the use of computer solutions such as the one here, their solutions will not be guaranteed to be optimal.
The
Gear Train Calculator can also perform reverted gear train solutions. The method for that function are considerably different than the one described here so far.