Happiness
- 686
- 30
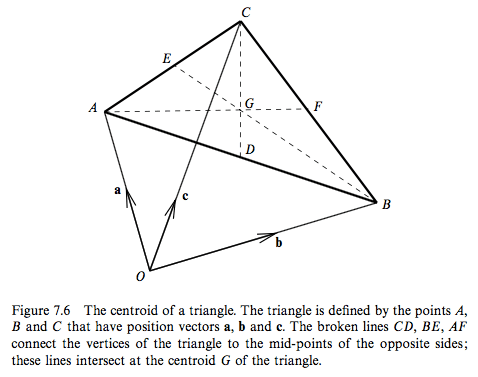
The position vector of the center of mass of a triangle is ##\frac{1}{3}(\mathbf{a}+\mathbf{b}+\mathbf{c})##.
Is the position vector of the center of mass of a planar four-sided figure ABCD ##\frac{1}{4}(\mathbf{a}+\mathbf{b}+\mathbf{c}+\mathbf{d})##? Does this generalise to n-sided figure?
How about a 3D figure ABCD in the form of an arbitrary triangular pyramid (whose faces need not be equilateral)? Is the center of mass also ##\frac{1}{4}(\mathbf{a}+\mathbf{b}+\mathbf{c}+\mathbf{d})##? Does this generalise to n-dimensonal figure?
Is the position vector of the center of mass of a planar four-sided figure ABCD ##\frac{1}{4}(\mathbf{a}+\mathbf{b}+\mathbf{c}+\mathbf{d})##? Does this generalise to n-sided figure?
How about a 3D figure ABCD in the form of an arbitrary triangular pyramid (whose faces need not be equilateral)? Is the center of mass also ##\frac{1}{4}(\mathbf{a}+\mathbf{b}+\mathbf{c}+\mathbf{d})##? Does this generalise to n-dimensonal figure?